Hoạt động2
Trả lời câu hỏi Hoạt động 2 trang 58
Trong không gian, cho 2 vec tơ \(\vec a\)và\(\vec b\) . Lấy một điểm A tùy ý.
a) Vẽ \(\overrightarrow {AB} \)\( = \vec a\),\(\overrightarrow {BC} \)\( = \vec b\)
b) Tổng của 2 vec tơ \(\vec a\)và\(\vec b\) bằng vec tơ nào trong hình 4?
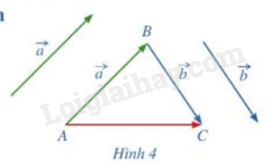

a) Ghi rõ các bước để vẽ hình
b) Áp dụng quy tắc 3 điểm \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)

a) – Qua A vẽ một đường thẳng song song với \(\vec a\) . Trên đường thẳng đó lấy điểm B sao cho \(AB = \left| {\vec a} \right|\)
– Qua B vẽ một đường thẳng song song với \(\vec b\). Trên đường thẳng đó lấy điểm C sao cho \(BC = \left| {\vec b} \right|\)
b) Ta có: \(\vec a + \vec b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Hoạt động3
Trả lời câu hỏi Hoạt động 3 trang 59
Cho hình hộp ABCD.A’B’C’D’. Tìm liên hệ giữa \(\overrightarrow {AB} + \overrightarrow {AD} \) và \(\overrightarrow {AC} ;\;\overrightarrow {AC} + \overrightarrow {AA’} \) và \(\overrightarrow {AC’} \)
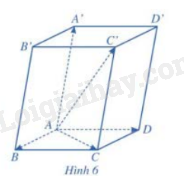

Áp dụng quy tắc ba điểm

Áp dụng quy tắc ba điểm ta thấy:
\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {BD} \) (1)
Mà từ hình vẽ ta thấy \(\overrightarrow {BD} = \overrightarrow {AC} \;\;\;\;\;\;\;\;\left( 2 \right)\)
Từ (1) (2) => \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
\(\overrightarrow {AC} + \overrightarrow {AA’} = \overrightarrow {A’C} \) (3)
Mà \(\overrightarrow {A’C} = \overrightarrow {AC’} \) (4)
Từ (3), (4) =>\(\overrightarrow {AC} + \overrightarrow {AA’} = \overrightarrow {AC’} \)
Hoạt động4
Trả lời câu hỏi Hoạt động 4 trang 59
Trong không gian , cho hai vecto\(\;\vec a,\vec b.\;\) Lấy một điểm M tùy ý
a) Vẽ \(\overrightarrow {MA} = \vec a,\;\overrightarrow {MB} = \vec b\; ,\overrightarrow {MC} = \overrightarrow { - b} \)
b) Tổng của hai vecto \(\vec a\;\)và \(\;\overrightarrow { - b} \) bằng vecto nào trong hình 7
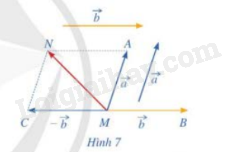


Advertisements (Quảng cáo)
Vì \(\overrightarrow { - CM} = \overrightarrow {NA} \) ; \(\overrightarrow {NA} + \overrightarrow {MA} = \overrightarrow {MN} \)
\(\vec a + \overrightarrow {\left( { - b} \right)} = \overrightarrow {MN} \)
Hoạt động5
Trả lời câu hỏi Hoạt động 5 trang 60
Nêu định nghĩa tích của một số thực \(k \ne 0\;\)với vecto\(\;\vec a\; \ne \vec 0\) trong mặt phẳng


Cho số thực \(k \ne 0\) và \(vecto\;\vec a \ne \vec 0\). Tích của số k với vecto \(\vec a\) là một vecto, kí hiệu là \(k\vec a,\;\)được xác định như sau
+, Cùng hướng với vecto \(\vec a\) nếu k\( > 0,\;\)ngược hướng với vecto \(\vec a\) nếu k<0
+, Có độ dài bằng \(\left| k \right|.\left| {\vec a} \right|\)
Hoạt động6
Trả lời câu hỏi Hoạt động 6 trang 61
Trong không gian, cho hai vecto \(\vec a,\vec b\)khác \(\;\vec 0\). Lấy một điểm O tùy ý.
a, Vẽ hai vecto \(\overrightarrow {OA} = \vec a,\;\overrightarrow {OB} = \vec b\)
b, Khi đó , hai vecto \(\overrightarrow {OA} ,\overrightarrow {OB} \) có giá nằm trong cùng mặt phẳng (P) (hình 10). Nếu định nghĩa góc giữa hai vecto \(\overrightarrow {OA} ,\;\overrightarrow {OB} \) trong hai mặt phẳng (P)
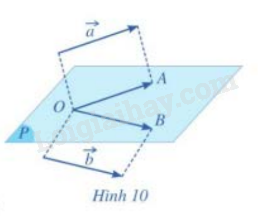


Trong không gian, cho hai vecto
\(\vec a,\vec b\)khác \(\;\vec 0\). Lấy một điểm O tùy ý và vẽ hai vecto\(\;\overrightarrow {OA} = \vec a,\overrightarrow {OB} = \vec b\). Góc giữa hai vecto \(\vec a,\overrightarrow {b\;} \) trong không gian, ký hiệu \(\left( {\vec a,\vec b} \right)\), là góc giữa hai vecto \(\;\overrightarrow {OA} ,\overrightarrow {OB} \)
Hoạt động7
Trả lời câu hỏi Hoạt động 7 trang 61
Trong không gian , cho hình lập phương ABCD.A’B’C’D’ có độ dài bằng 3cm (hình 12)
a, Tính góc giữa hai vecto \(\overrightarrow {AC} ,\overrightarrow {A’D’} \)
b, Tính \(\left| {\overrightarrow {AC} } \right|,\left| {\overrightarrow {A’D’} } \right|\). Cos(\(\overrightarrow {AC} ,\overrightarrow {A’D’} \))
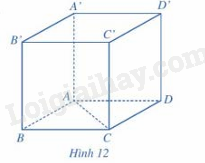

Áp dụng quy tăc 3 điểm và vectơ trong không gian

Ta có A’D’//AD
Góc giữa \(\overrightarrow {AC} \;\)và\(\;\overrightarrow {A’D’} \)= \(\;\overrightarrow {AC} \) và \(\overrightarrow {AD} \)
a, Mà ABCD là hình vuông => \(\widehat {CAD} = 45^\circ \)
b, \(\overrightarrow {\left| {AC} \right|} .|\overrightarrow {A’D’|} \)=AC.AD= 3.3=9
Cos(\(\overrightarrow {AC} ,\overrightarrow {A’D’} \))= cos(\(\overrightarrow {AC} ,\overrightarrow {AD} )\)= \(\frac{{\overrightarrow {AC} .\overrightarrow {AD} }}{{\overrightarrow {\left| {AC} \right|} .\overrightarrow {\left| {AD} \right|} }} = \frac{{3.3}}{{3.3}} = 1\)
