Câu hỏi/bài tập:
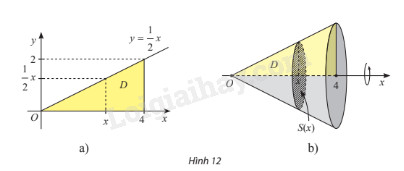
Cho \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right) = \frac{1}{2}x\), trục hoành và đường thẳng \(x = 4\) (hình 12a). Quay hình \(D\) xung quanh trục \(Ox\) thì được một khối nón, kí hiệu là \(N\). (hình 12b)
a) Cắt khối \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( {0 \le x \le 4} \right)\) thì mặt cắt là hình gì? Tính diện tích \(S\left( x \right)\) của mặt cắt đó.
b) Sử dụng công thức tính thể tích hình khối, tính thể tích của khối nón \(N\).

Advertisements (Quảng cáo)
a) Mặt cắt khi cắt khối nón \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) là hình tròn. Tính bán kính của hình tròn, từ đó tính được diện tích \(S\left( x \right)\) của mặt cắt đó.
b) Công thức tính thể tích của khối nón \(N\) có bán kính đáy \(r\) và chiều cao \(h\): \(V = \frac{1}{3}\pi {r^2}h\).

a) Mặt cắt khi cắt khối nón \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) là hình tròn. Ta nhận thấy rằng khi cắt khối nón \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) thì bán kính mặt cắt sẽ là \(\frac{1}{2}x\).
Do đó diện tích của mặt cắt là \(S\left( x \right) = \pi .{\left( {\frac{1}{2}x} \right)^2} = \frac{\pi }{2}{x^2}\).
b) Khối nón \(N\) có bán kính đáy \(r = 2\) và chiều cao \(h = 4\) nên thể tích của khối nón là: \(V = \frac{1}{3}\pi {.2^2}.4 = \frac{{16\pi }}{3}\)
