
Tìm cực trị của các hàm số sau:a) \(y = 2{x^3} - 9{x^2} + 12x - 5\);\(y = {x^4} - 4{x^2} + 2\)b) ;c) \(y = \frac{{{x^2} - 2x + 3}}{{x - 1}}\);d) \(y = \sqrt {4x - 2{x^2}} \).

Sử dụng kiến thức về cách tìm cực trị của hàm số để tìm cực trị của hàm số \(y = f\left( x \right)\):
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm f’(x). Tìm các điểm mà tại đó đạo hàm f’(x) bằng 0 hoặc đạo hàm không tồn tại.
3. Lập bảng biến thiên của hàm số.
4. Từ bảng biến thiên suy ra các cực trị của hàm số.

a) Tập xác định: \(D = \mathbb{R}\).
\(y’ = 6{x^2} - 18x + 12\), \(y’ = 0 \Leftrightarrow 6{x^2} - 18x + 12 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\)
Bảng biến thiên:
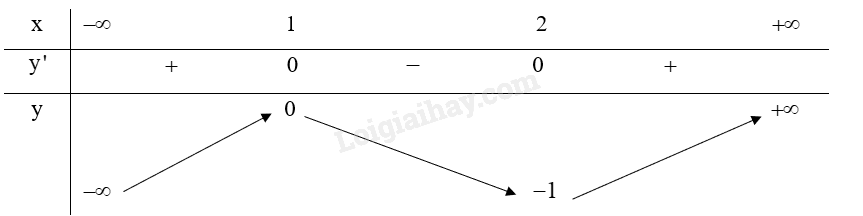
Từ bảng biến thiên ta có:
Hàm số \(y = 2{x^3} - 9{x^2} + 12x - 5\) có điểm cực đại là \(\left( {1;0} \right)\).
Hàm số \(y = 2{x^3} - 9{x^2} + 12x - 5\) có điểm cực tiểu là \(\left( {2; - 1} \right)\).
b) Tập xác định của hàm số là \(\mathbb{R}\).
Ta có: \(y’ = 4{x^3} - 8x,y’ = 0 \Leftrightarrow 4{x^3} - 8x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt 2 \end{array} \right.\)
Bảng biến thiên:
Advertisements (Quảng cáo)
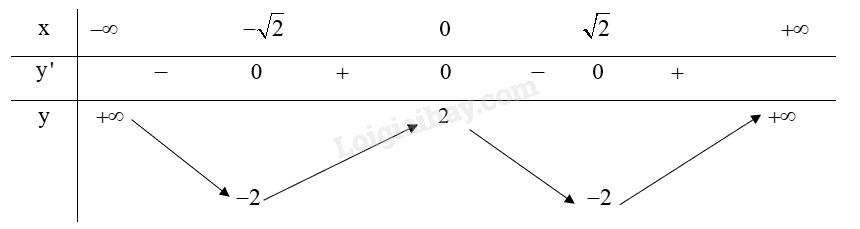
Từ bảng biến thiên ta có:
Hàm số \(y = {x^4} - 4{x^2} + 2\) đạt cực đại tại \(x = 0\) và .
Hàm số \(y = {x^4} - 4{x^2} + 2\) đạt cực tiểu tại \(x = \pm \sqrt 2 \) và \({y_{CT}} = - 2\).
c) Tập xác định: \(D = \mathbb{R}\backslash \left\{ 1 \right\}\).
Ta có: \(y’ = \frac{{\left( {2x - 2} \right)\left( {x - 1} \right) - \left( {{x^2} - 2x + 3} \right)}}{{{{\left( {x - 1} \right)}^2}}} = \frac{{{x^2} - 2x - 1}}{{{{\left( {x - 1} \right)}^2}}}\)
\(y’ = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 - \sqrt 2 \\x = 1 + \sqrt 2 \end{array} \right.\) (thỏa mãn)
Lập bảng biến thiên của hàm số:
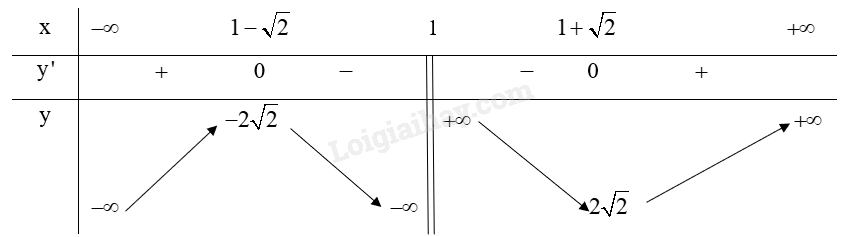
Từ bảng biến thiên ta có:
Hàm số \(y = \frac{{{x^2} - 2x + 3}}{{x - 1}}\) đạt cực đại tại \(x = 1 - \sqrt 2 \) và .
Hàm số \(y = \frac{{{x^2} - 2x + 3}}{{x - 1}}\) đạt cực tiểu tại \(x = 1 + \sqrt 2 \) và \({y_{CT}} = 2\sqrt 2 \).
d) \(y = \sqrt {4x - 2{x^2}} \)
Tập xác định: \(D = \left[ {0;2} \right]\).
Ta có: \(y’ = \frac{{\left( {4x - 2{x^2}} \right)’}}{{2\sqrt {4x - 2{x^2}} }} = \frac{{ - x + 1}}{{\sqrt {4x - 2{x^2}} }},y’ = 0 \Leftrightarrow x = 1\left( {tm} \right)\)
Ta có bảng biến thiên của hàm số:
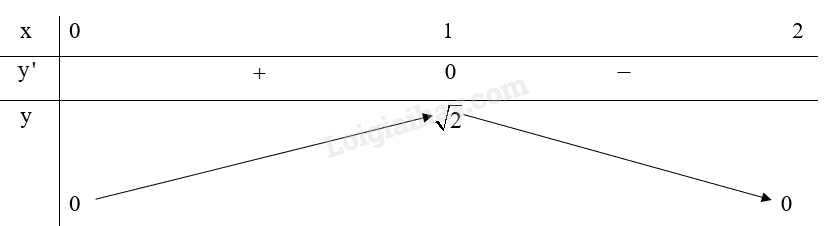
Do đó, hàm số đạt cực đại tại \(x = 1\), hàm số không có cực tiểu.
