Câu hỏi/bài tập:

Tính diện tích của hình phẳng được tô màu trong Hình 4.29.
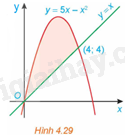

Advertisements (Quảng cáo)
Sử dụng kiến thức về diện tích hình phẳng giới hạn bởi hai đồ thị hàm số và đường thẳng \(x = a,x = b\) để tính: Diện tích S của hình phẳng giới hạn đồ thị của hai hàm số f(x), g(x) liên tục trên đoạn [a; b] và hai đường thẳng \(x = a,x = b\), được tính bằng công thức \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).

Diện tích hình phẳng cần tính là:
\(S = \int\limits_0^4 {\left| {5x - {x^2} - x} \right|dx} = \int\limits_0^4 {\left| { - {x^2} + 4x} \right|dx} = \int\limits_0^4 {\left( { - {x^2} + 4x} \right)dx} = \left( {\frac{{ - {x^3}}}{3} + 2{x^2}} \right)\left| \begin{array}{l}4\\0\end{array} \right. = \frac{{ - {4^3}}}{3} + {2.4^2} = \frac{{32}}{3}\)
