Sử dụng kiến thức về dạng của đồ thị hàm số để chọn đáp án. Hướng dẫn giải Giải bài tập 4 trang 90 SGK Toán 12 tập 2 - Kết nối tri thức - Bài tập ôn tập cuối năm . Đường cong trong hình bên là đồ thị của một trong bốn hàm số dưới đây.
Câu hỏi/bài tập:

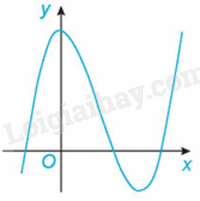
Đường cong trong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
A. \(y = - {x^3} + 3{x^2} + 1\).
B. \(y = {x^3} - 3{x^2} + 3\).
C. \(y = - {x^2} + 2x + 1\).
D. \(y = \frac{{x + 1}}{{x - 1}}\).
Advertisements (Quảng cáo)

Sử dụng kiến thức về dạng của đồ thị hàm số để chọn đáp án.

Đây là là dạng của đồ thị hàm số bậc ba nên đáp án C, D sai.
Đồ thị hàm số trong hình vẽ đồng biến trên khoảng \(\left( { - \infty ;0} \right)\).
Xét hàm số: \(y = {x^3} - 3{x^2} + 3\) ta có: \(y’ = 3{x^2} - 6x,y’ = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\)
Do đó, hàm số \(y = {x^3} - 3{x^2} + 3\) đồng biến trên khoảng \(\left( { - \infty ;0} \right)\).
Chọn B
