Có nhận xét gì về mối quan hệ giữa $\sin \left( {\Delta ,\Delta ‘} \right)$ và $\left| {\cos \left( {\ u ,\ n } \right)} \right|$?...

Trong không gian Oxyz, cho đường thẳng $\Delta$ và mặt phẳng (P). Xét $\overrightarrow u = \left( {a;b;c} \right)$ là một vectơ chỉ phương của $\Delta$ và $\overrightarrow n = \left( {A;B;C} \right)$ (với giá $\Delta ‘$) là một vectơ pháp tuyến của (P). (H.5.35)

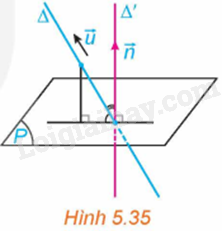
a) Hãy tìm mối quan hệ giữa các góc $\left( {\Delta ,\left( P \right)} \right)$ và $\left( {\Delta ,\Delta ‘} \right)$.

b) Có nhận xét gì về mối quan hệ giữa $\sin \left( {\Delta ,\Delta ‘} \right)$ và $\left| {\cos \left( {\overrightarrow u ,\overrightarrow n } \right)} \right|$?

Sử dụng kiến thức giá của vectơ để chứng minh: Đường thẳng đi qua điểm đầu và điểm cuối của vectơ được gọi là giá của vectơ đó.

a) Mối quan hệ của góc $\left( {\Delta ,\left( P \right)} \right)$ và $\left( {\Delta ,\Delta ‘} \right)$ là: $\left( {\Delta ,\left( P \right)} \right) = {90^0} - \left( {\Delta ,\Delta ‘} \right)$

b) Ta có: +) $\left( {\Delta ,\left( P \right)} \right) = {90^0} - \left( {\Delta ,\Delta ‘} \right) = {90^0} - \left( {\overrightarrow u ,\overrightarrow n } \right)$ với $\left( {\overrightarrow u ,\overrightarrow n } \right) \le {90^o}$

+) $\left( {\Delta ,\left( P \right)} \right) = {90^0} - \left( {\Delta ,\Delta ‘} \right) = {90^0} - \left[ {{{180}^o} - \left( {\overrightarrow u ,\overrightarrow n } \right)} \right] = - {90^o} + \left( {\overrightarrow u ,\overrightarrow n } \right)$ với $\left( {\overrightarrow u ,\overrightarrow n } \right) > {90^o}$

Suy ra, $\sin \left( {\Delta ,\Delta ‘} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow n } \right)} \right|$.