Bài 11.
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số
\(y = {{x + 3} \over {x + 1}}\)
b) Chứng minh rằng với mọi giá trị của \(m\), đường thẳng \(y = 2x + m\) luôn cắt \((C)\) tại hai điểm phân biệt \(M\) và \(N\)
c) Xác định m sao cho độ dài \(MN\) là nhỏ nhất
d) Tiếp tuyến tại một điểm \(S\) bất kì của \((C)\) luôn cắt hai tiệm cận của \((C)\) tại \(P\) và \(Q\). Chứng minh rằng \(S\) là trung điểm của \(PQ\).
a) \(y = {{x + 3} \over {x + 1}}\)
Tập xác định : \(D=\mathbb R\backslash {\rm{\{ }} - 1\} \)
* Sự biến thiên:
\(y’ = {{ - 2} \over {{{(x + 1)}^2}}} < 0,\forall x \in D\)
- Hàm số nghịch biến trên khoảng: \((-\infty;-1)\) và \((-1;+\infty)\)
- Cực trị: Hàm số không có cực trị.
- Tiệm cận:
\(\eqalign{
& \mathop {\lim }\limits_{x \to - {1^ - }} y = - \infty \cr
& \mathop {\lim }\limits_{x \to - {1^ + }} y = + \infty \cr
& \mathop {\lim }\limits_{x \to \pm \infty } y = 1 \cr} \)
Tiệm cận đứng: \(x = -1\)
Tiệm cận ngang: \(y = 1\)
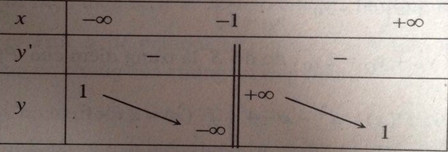
Bảng biến thiên:
Advertisements (Quảng cáo)
* Đồ thị:
Đồ thị hàm số giao \(Ox\) tại \((-3;0)\), giao \(Oy\) tại \((0;3)\)
Đồ thị hàm số nhận điểm \(I(-1;1)\) làm tâm đối xứng.
b) Xét phương trình có nghiệm là hoành độ giao điểm của \((C)\) và đường thẳng (d): \(y = 2x + m\) (1)
\(\eqalign{
& {{x + 3} \over {x + 1}} = 2x + m \Leftrightarrow x + 3 = (2x + m)(x + 1) \cr
& \Leftrightarrow 2{x^2} + (m + 1)x + m - 3 = 0,x \ne - 1 \cr} \)
\(Δ = (m+1)^2– 4.2(m-3) = m^2– 6m + 25 = (m-3)^2+ 16> 0\), nên (1) luôn có hai nghiệm phân biệt khác \(-1\).
Vậy (d) luôn cắt (C) tại hai điểm phân biệt \(M, N\) (hoành độ của \(M, N\) chính là nghiệm của (1)).
c) Theo định lí Vi-et ta có:
\(\left\{ \matrix{
{x_M} + {x_N} = - {{m + 1} \over 2} \hfill \cr
{x_M}.{x_N} = {{m - 3} \over 2} \hfill \cr} \right.\)
\(\eqalign{
& M{N^2} = {\rm{ }}{\left( {{x_M}-{x_N}} \right)^2} + {\rm{ }}{({y_M} - {\rm{ }}{y_N})^2} \cr
& = {\left( {{x_M}-{x_N}} \right)^2} + {\left[ {(2{x_M} + m) - (2{x_N} + m)} \right]^2} \cr
& = 5{\left( {{x_M}-{x_N}} \right)^2} = 5\left[ {{{\left( {{x_M}+{x_N}} \right)}^2} - 4{x_M}{x_N}} \right] \cr
& = 5\left[ {{{( - {{m + 1} \over 2})}^2} - 4.{{m - 3} \over 2}} \right] = {5 \over 4}({m^2} - 6m + 25) \cr
& = {5 \over 4}\left[ {{{(m - 3)}^2} + 16} \right] \ge {5 \over 4}.16 = 20 \cr} \)
\(MN = 2\sqrt5 ⇔ m = 3\)
Vậy độ dài \(MN\) nhỏ nhất bằng \(2\sqrt5\) khi \(m=3\)
d) Giả sử \(S(x_0;y_0)\) là điểm bất kì thuộc (C)
Phương trình tiếp tuyến \(Δ\) của (C) tại \(S\) là:
\(\eqalign{
& y - y = y'({x_0})(x - {x_0}) \cr
& \Leftrightarrow y = {{ - 2} \over {{{({x_0} + 1)}^2}}}(x - {x_0}) + {{{x_0} + 3} \over {{x_0} + 1}} \cr} \)
\(Δ\) cắt tiệm cận ngang tại \(P(2x_0+ 1, 1)\), \(Δ\) cắt tiệm cận đứng tại \(Q( - 1,{y_0} + {2 \over {{x_0} + 1}})\)
Rõ ràng: \({x_P} + {x_Q} = 2{x_0},{y_P} + {y_Q} = 2{y_0}\). Do đó, \(S\) là trung điểm của \(PQ\).
