Bài 7.
a) Khảo sát sự biến thiên và vẽ đồ thị \((C)\) của hàm số:
\(y = x^3+ 3x^2+ 1\)
b) Dựa vào đồ thị \((C)\), biện luận số nghiệm của phương trình sau theo m
\({x^3} + 3{x^2} + 1 = {m \over 2}\)
c) Viết phương trình đường thẳng đi qua điểm cực đại và điểm cực tiểu của đồ thị \((C)\)
a) \(y = x^3+ 3x^2+ 1\)
Tập xác định: \(D =\mathbb R\)
* Sự biến thiên:
\(y’= 3x^2+ 6x = 3x(x+ 2)\)
\(y’=0 ⇔ x = 0, x = -2\).
- Hàm số đồng biến trên khoảng \((-\infty;-2)\) và \((0;+\infty)\), nghịch biến trên khoảng \((-2;0)\)
- Cực trị:
Hàm số đạt cực đại tại \(x=-2\); \(y_{CĐ}=5\)
Hàm số đạt cực tiểu tại \(x=0\); \(y_{CT}=1\).
- Giới hạn:
Advertisements (Quảng cáo)
\(\eqalign{
& \mathop {\lim }\limits_{x \to - \infty } y = - \infty \cr
& \mathop {\lim }\limits_{x \to + \infty } y = + \infty \cr} \)
- Bảng biến thiên:
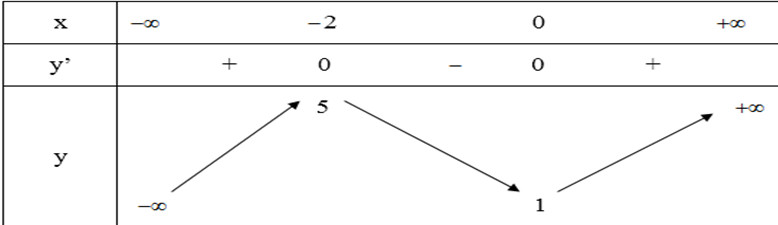
Đồ thị:
Đồ thị hàm số giao \(Oy\) tại \((0;1)\)
Đồ thị hàm số nhận \(I(-1;3)\) làm tâm đối xứng.
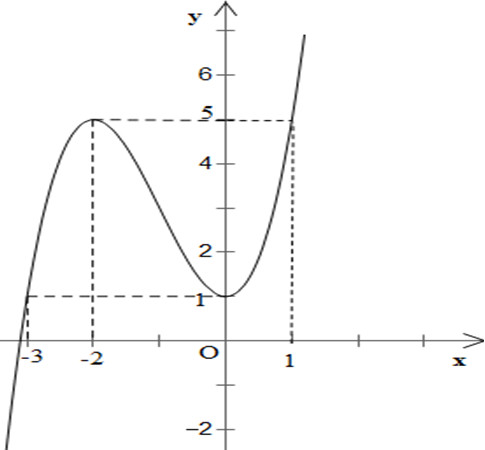
b) Số nghiệm của phương trình \({x^3} + 3{x^2} + 1 = {m \over 2}\) chính là số giao điểm của \((C)\) và đường thẳng \((d)\): \(y = {m \over 2}\)
Từ đồ thị ta thấy:
- Với \({m \over 2} < 1 \Leftrightarrow m < 2\) : (d) cắt (C) tại 1 điểm, phương trình có 1 nghiệm
- Với \({m \over 2} = 1 ⇔ m = 2\): (d) tiếp xúc với (C) tại 1 điểm và cắt (C) tạo 1 điểm, phương trình có hai nghiệm
- Với \(1 < {m \over 2} < 5 ⇔ 2<m<10\), phương trình có 3 nghiệm.
- Với \({m \over 2} = 5 \Leftrightarrow m = 10\): (d) cắt (C) tại 1 điểm và tiếp xúc với (C) tại 1 điểm, phương trình có hai nghiệm.
- Với \({m \over 2} > 5 \Leftrightarrow m > 10\) : (d) cắt (C) tại 1 điểm, phương trình có 1 nghiệm
c) Điểm cực đại \((-2, 5)\), điểm cực tiểu \((0, 1)\).
Đường thẳng đi qua hai điểm này có phương trình là: \({{y - 1} \over 4} = {x \over { - 2}} \Leftrightarrow y = - 2x + 1\)
