
Cho ∆ABC = ∆MNP. Hai tia phân giác của góc B và C cắt nhau tại O tạo thành góc BOC bằng 120°. Tính tổng số đo các góc MNP và MPN của tam giác MNP.

Hai tam giác bằng nhau suy ra các góc tương ứng bằng nhau.

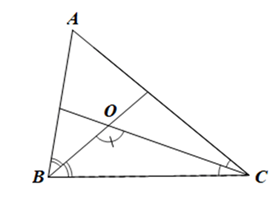
Vì BO là phân giác của góc ABC nên\(\widehat {ABO} = \widehat {CBO} = \frac{{\widehat {ABC}}}{2}\)
Vì CO là phân giác của góc ACB nên \(\widehat {ACO} = \widehat {BCO} = \frac{{\widehat {ACB}}}{2}\)
Advertisements (Quảng cáo)
Xét DCOB ta có: \(\widehat {BOC} + \widehat {OBC} + \widehat {OCB} = 180^\circ \) (tổng ba góc của một tam giác)
Suy ra \(\widehat {OBC} + \widehat {OCB} = 180^\circ - \widehat {BOC} = 180^\circ - 120^\circ = 60^\circ .\)
Mà \(\widehat {CBO} = \frac{{\widehat {ABC}}}{2},\widehat {BCO} = \frac{{\widehat {ACB}}}{2}.\)
Suy ra \(\frac{{\widehat {ABC}}}{2} + \frac{{\widehat {ACB}}}{2} = 60^\circ \)
Do đó \(\widehat {ABC} + \widehat {ACB} = 2.60^\circ = 120^\circ .\)
Mặt khác ∆ABC = ∆MNP nên ta có:
\(\widehat {ABC} = \widehat {MNP}\) và \(\widehat {ACB} = \widehat {MPN}\) (các cặp góc tương ứng).
Suy ra \(\widehat {MNP} + \widehat {MPN} = \widehat {ABC} + \widehat {ACB} = 120^\circ \)
Vậy \(\widehat {MNP} + \widehat {MPN} = 120^\circ \)
