
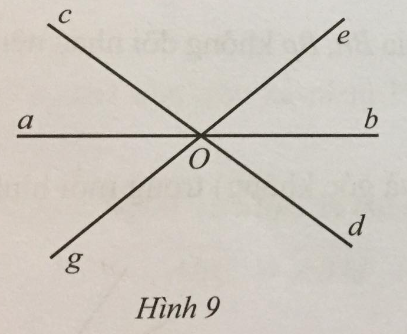
Quan sát Hình 9.
a) Hai góc aOg và cOe có phải là hai góc đối đỉnh hay không? Vì sao?
b) Tìm các cặp đối đỉnh (khác góc bẹt và góc không) ở Hình 9.
c) Chứng tỏ rằng \(\widehat {aOg} + \widehat {cOe} + \widehat {bOd} = 180^\circ \).

Advertisements (Quảng cáo)
a), b) Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
c) Chứng tỏ tổng ba góc bằng 180° dựa vào hai góc đối đỉnh có số đo góc bằng nhau.

a) Hai góc aOg và cOe không phải là hai góc đối đỉnh. Vì Og và Oe là hai tia đối nhưng Oa và Oc không là hai tia đối.
b) Các cặp góc đối đỉnh là aOc và bOd, cOe và dOg, bOe và aOg, aOe và bOg, bOc và aOd, cOg và dOe.
c) Ta có: \(\widehat {aOc} = \widehat {bOd}\) (đối đỉnh)
nên: \(\widehat {aOg} + \widehat {cOe} + \widehat {bOd} = \widehat {aOg} + \widehat {cOe} + \widehat {aOc} = \widehat {gOe} = 180^\circ \).
