
Chứng minh rằng các đường trung trực của tam giác vuông đi qua trung điểm của cạnh huyền.

Gọi d là đường trung trực của cạnh AB và M là giao điểm của d và BC.
Chứng minh M là trung điểm của BC

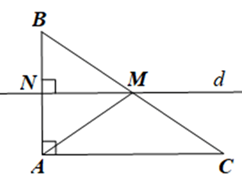
Gọi d là đường trung trực của cạnh AB và M là giao điểm của d và BC.
Advertisements (Quảng cáo)
Do M ∈ d nên MA = MB hay tam giác MAB cân tại M.
Suy ra \(\widehat {MBA} = \widehat {MAB}\) (1)
Trong tam giác vuông ABC có \(\widehat {ABC} + \widehat {ACB} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Nên \(\widehat {ACB} = 90^\circ - \widehat {ABC}\) (2)
Ta có \(\widehat {BAM} + \widehat {MAC} = \widehat {BAC} = 90^\circ \)
Nên \(\widehat {MAC} = 90^\circ - \widehat {MBA}\) (3)
Từ (1),(2) và (3) suy ra \(\widehat {MAC} = \widehat {MCA}\)
Do đó tam giác MAC cân tại M nên MA = MC.
Như vậy, MB = MC (= MA) nên M là trung điểm của BC.
Vậy các đường trung trực của tam giác vuông đi qua trung điểm của cạnh huyền.
