
Tam giác ABC có ba đường trung tuyến cắt nhau tại G. Biết rằng điểm G cũng là giao điểm của ba đường trung trực trong tam giác ABC. Chứng minh tam giác ABC đều.

Chứng minh tam giác ABC đều bằng cách chứng minh AB = BC = CA.

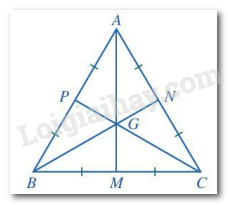
Gọi M, N, P lần lượt là các trung điểm của các đoạn thẳng BC, AC, AB.
Ta có: G là giao điểm của ba đường trung tuyến trong tam giác ABC.
Advertisements (Quảng cáo)
Mà G cũng là giao điểm của ba đường trung trực trong tam giác ABC nên AM, BN, CP là các đường trung trực của tam giác ABC hay \(AM \bot BC;BN \bot AC;CP \bot AB\).
Xét tam giác ABM và tam giác ACM có:
AM chung;
\(\widehat {AMB} = \widehat {AMC} (= 90^\circ \))(vì \(AM \bot BC\));
BM = MC (M là trung điểm của BC).
Vậy \(\Delta ABM = \Delta ACM\)(c.g.c). Suy ra: AB = AC ( 2 cạnh tương ứng). (1)
Tương tự ta có:
\(\Delta BNA = \Delta BNC\)(c.g.c). Suy ra: AB = BC( 2 cạnh tương ứng). (2)
Từ (1) và (2) suy ra: AB = BC = AC.
Vậy tam giác ABC đều.
