
Tam giác ABC có ba đường phân giác cắt nhau tại I. Biết rằng I cũng là giao điểm ba đường trung trực của tam giác ABC. Chứng minh tam giác ABC đều.

Chứng minh tam giác ABC đều bằng cách chứng minh AB = BC = CA.

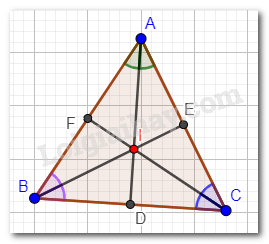
Ta có: I là giao điểm của ba đường phân giác của tam giác ABC. Đồng thời là giao điểm của ba đường trung trực tam giác ABC nên: \(ID \bot BC;IE \bot AC;IF \bot AB\).
Advertisements (Quảng cáo)
Xét tam giác ADB và tam giác ADC có:
\(\widehat {BAD} = \widehat {CAD}\)(AD là phân giác của góc A);
AD chung;
\(\widehat {ADB} = \widehat {ADC}(=90^0)\)(vì \(ID \bot BC\)).
Vậy \(\Delta ADB = \Delta ADC\)(g.c.g). Suy ra: AB = AC ( 2 cạnh tương ứng). (1)
Tương tự ta có: \(\Delta BEA = \Delta BEC\)(g.c.g). Suy ra: BA = BC ( 2 cạnh tương ứng). (2)
Từ (1) và (2) suy ra: AB = BC = AC.
Vậy tam giác ABC đều.
