
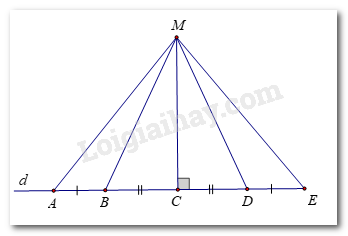
Cho 5 điểm A, B, C, D, E cùng nằm trên một đường thẳng d sao cho AB = DE, BC = CD. Điểm M không thuộc d sao cho MC vuông góc với d. Chứng minh rằng:
a)\(\Delta MBC = \Delta MDC,\Delta MAC = \Delta MEC\)
b)\(\Delta MAB = \Delta MED\)

-Chứng minh:
\(\begin{array}{l}\Delta MBC = \Delta MDC\left( {c - g - c} \right),\\\Delta MAC = \Delta MEC\left( {c - g - c} \right)\end{array}\)
-Áp dụng kết quả ý a, chứng minh b) \(\Delta MAB = \Delta MED\left( {c - c - c} \right)\)

Advertisements (Quảng cáo)
a)
-Xét \(\Delta MBC\) và \(\Delta MDC\)có:
\(\begin{array}{l}\widehat {MCB} = \widehat {BCD} = {90^0}\\BC = CD\left( {gt} \right)\\MC:chung\\ \Rightarrow \Delta MBC = \Delta MDC\left( {c - g - c} \right)\\ \Rightarrow MB = MD\left( {ctu} \right)\end{array}\)
-Xét \(\Delta MAC\) và \(\Delta MEC\)có:
\(\begin{array}{l}\widehat {MCA} = \widehat {MCE} = {90^0}\\MC:chung\\\left\{ \begin{array}{l}AC = AB + BC\\EC = DE + CD\end{array} \right.\\Do\,AB = DE;BC = CD\left( {gt} \right)\\ \Rightarrow AC = EC\\ \Rightarrow \Delta MAC = \Delta MEC\left( {c - g - c} \right)\\ \Rightarrow MA = ME\left( {ctu} \right)\end{array}\)
b)
Xét \(\Delta MAB\)và \(\Delta MED\)có:
MA = ME (cmt)
MB = MD (cmt)
AB = ED (gt) \( \Rightarrow \Delta MAB = \Delta MED\left( {c - c - c} \right)\)
