Chứng minh rằng tổng MA + MB + MC lớn hơn nửa chu vi tam giác ABC.. Câu 27 trang 41 Sách Bài Tập (SBT) Toán lớp 7 tập 2 - Bài 3: Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác
Cho điểm M nằm trong tam giác ABC. Chứng minh rằng tổng MA + MB + MC lớn hơn nửa chu vi tam giác ABC.

Trong ∆AMB ta có:
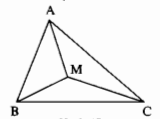
MA + MB > AB (bất đẳng thức tam giác) (1)
Trong ∆AMC ta có:
Advertisements (Quảng cáo)
MA + MC > AC (bất đẳng thức tam giác) (2)
Trong ∆BMC ta có:
MB + MC > BC (bất đẳng thức tam giác) (3)
Cộng từng vế của (1), (2) và (3) ta có:
2(MA + MB + MC) > AB + AC + BC
Suy ra: \(MA + MB + MC > {{AB + AC + BC} \over 2}\)
