Chứng minh.. Câu 30 trang 41 Sách Bài Tập (SBT) Toán lớp 7 tập 2 - Bài 3: Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác
Cho tam giác ABC. Gọi M là trung điểm của BC.
Chứng minh rằng \(AM < {{AB + AC} \over 2}\)

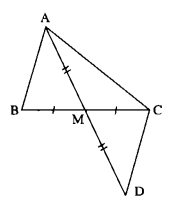
Trên tia đối của tia MA lấy điểm D sao cho MA = MD
Xét ∆AMB và ∆DMC:
MA = MD (theo cách vẽ)
\(\widehat {AMB} = \widehat {DMC}\) (đối đỉnh)
Advertisements (Quảng cáo)
MB = MC (gt)
Do đó: ∆AMB = ∆DMC (c.g.c)
\( \Rightarrow \) AB = BC (hai cạnh tương ứng)
Trong ∆ACD ta có:
AD < AC + CD (bất đẳng thức tam giác)
Mà AD = AM + MD = 2AM
CD = AB
\(2{\rm{A}}M < AC + AB \Rightarrow AM < {{AB + AC} \over 2}\)
