Câu 4.4 trang 44 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Trong tam giác ABC, hai đường trung tuyến \({\rm{A}}{{\rm{A}}_1}\) và \(B{B_1}\) cắt nhau tại điểm O. Hãy tính diện tích tam giác ABC nếu diện tích tam giác ABO bằng \(5c{m^2}\).
Giải
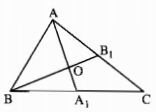
Ta có:
\({S_{AOB}} = {2 \over 3}{S_{{\rm{A}}{{\rm{A}}_1}B}}\) (Vì \({\rm{A}}O = {2 \over 3}{\rm{A}}{{\rm{A}}_1}\));
\({{\rm{S}}_{AB{A_1}}} = {1 \over 2}{S_{ABC}}\) (Vì \(B{A_1} = {1 \over 2}BC\)) ;
Từ đó suy ra \({{\rm{S}}_{ABC}} = 2{{\rm{S}}_{AB{A_1}}} = 3{{\rm{S}}_{AOB}}\)
Nếu \({{\rm{S}}_{AOB}} = 5c{m^2}\) thì \({S_{ABC}} = 3.5 = 15\left( {c{m^2}} \right)\)
Câu 4.5 trang 44 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Chứng minh rằng các trung tuyến của một tam giác phân chia tam giác đó thành 6 tam giác mà diện tích của chúng (đôi một) bằng nhau.
Giải
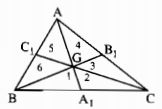
Xét sáu tam giác được đánh số là: 1, 2, 3, 4, 5, 6
Chứng minh hoàn toàn tương tự như bài 4.4 ta có
\({S_{GAB}} = {S_{GBC}} = {S_{GCA}} = {1 \over 3}{S_{ABC}}\)
Ta lại có \({{\rm{S}}_1} = {S_2},{S_3} = {S_4},{S_5} = {S_6}\) (vì mỗi cặp tam giác có chung đường cao và hai đáy bằng nhau, vậy sáu tam giác 1, 2, 3, 4, 5, 6 có diện tích bằng nhau)
Câu 4.6 trang 44 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Cho tam giác ABC với đường trung tuyến AD. Trên tia AD lấy điểm E sao cho AD = DE, trên tia BC lấy điểm M sao cho BC = CM.
Advertisements (Quảng cáo)
a) Tìm trọng tâm của tam giác AEM.
b) So sánh các cạnh của tam giác ABC với các đường trung tuyến của tam giác AEM
c) So sánh các đường trung tuyến của tam giác ABC với các cạnh của tam giác AEM.
Giải
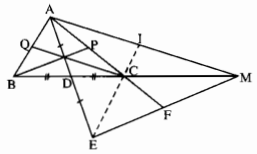
a) Do AD = DE nên MD là một đường trung tuyến của tam giác AEM. Hơn nữa do
$$C{\rm{D}} = {1 \over 2}CB = {1 \over 2}CM$$
Nên C là trọng tâm của tam giá AEM.
b) Các đường thẳng AC, EC lần lượt cắt EM, AM tại F, I. Tam giác AEM có các đường trung tuyến là AF, EI, MD. Ta có ∆ADB = ∆EDG (c.g.c) nên AB = EC
Vậy: \(AC = {2 \over 3}{\rm{AF;BC = CM = }}{2 \over 3}{\rm{MD}};AB = EC = {2 \over 3}EI\)
c) Trước tiên, theo giả thiết, ta có AD = DE nên \(A{\rm{D}} = {1 \over 2}A{\rm{E}}\)
Gọi BP, CQ là các trung tuyến của ∆ABC.
∆BCP = ∆MCF => \(BP = FM = {1 \over 2}EM\). Ta sẽ chứng minh \(CQ = {1 \over 2}AM\)
Ta có:
\(\eqalign{
& \Delta AB{\rm{D}} = \Delta EC{\rm{D}} \Rightarrow \widehat {BA{\rm{D}}} = \widehat {CED} \cr
& \Rightarrow AB//EC \Rightarrow \widehat {QAC} = \widehat {IC{\rm{A}}} \cr} \)
Hai tam giác ACQ và CAI có cạnh AC chung, \(\widehat {QAC} = \widehat {IC{\rm{A}}}\);
\(AQ = {1 \over 2}AB = {1 \over 2}EC = IC\) nên chúng bằng nhau.
Vậy \(CQ = AI = {1 \over 2}AM\).
Tóm lại: \(A{\rm{D}} = {1 \over 2}A{\rm{E,BP = }}{1 \over 2}{\rm{EM,CQ = }}{1 \over 2}{\rm{AM}}\)
