Câu 2.1 trang 39Sách Bài Tập (SBT) Toán lớp 7 tập 2
Cho đường thẳng d và điểm A không thuộc d. Trong các khẳng định sau đây, khẳng định nào đúng, khẳng định nào sai?
(A) Có duy nhất một đường vuông góc kẻ từ điểm A đến đường thẳng d.
(B) Có duy nhất một đường kẻ xiên kẻ từ điểm A đến đường thẳng d.
(C) Có vô số đường vuông góc kẻ từ điểm A đến đường thẳng d.
(D) Có vô số đường kẻ xiên kẻ từ điểm A đến đường thẳng d.
Hãy vẽ hình minh họa cho các khẳng định đúng.
Giải
Ta biết rằng có duy nhất một đường thẳng đi qua một điểm cho trước, vuông góc với một đường thẳng cho trước và có vô số đường thẳng đi qua một điểm cho trước cắt một đường cho trước. Bởi vì, có duy nhất một đường vuông góc kẻ từ điểm A đến đường thẳng d và có vô số đường xiên kẻ từ điểm A đến đường thẳng d.
(A) Đúng (B) Sai
(C) Sai (D) Đúng
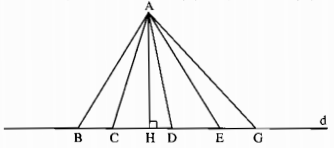
Trong hình AH là đường vuông góc duy nhất và AB, AC, AD, AE, AG là những đường xiên kẻ từ A đến d (có thể kẻ được vô số đường xiên như thế)
Câu 2.2 trang 39 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Qua điểm A không thuộc đường thẳng d, kẻ đường vuông góc AH và các đường xiên AB, AC đến đường thẳng d (H, B, C đều thuộc d). Biết rằng HB < HC. Hãy chọn khẳng định đúng trong các khẳng định sau:
(A) AB > AC (B) AB = AC
(C) AB > AC (D) AH > AB
Giải
Theo định lý so sánh giữa hình chiếu và hình xiên ta có:
Advertisements (Quảng cáo)
HB < HC => AB < AC. Chọn (C)
Câu 2.3 trang 39 Sách Bài Tập (SBT) Toán lớp7tập 2
a) Hai tam giác ABC, A’B’C’ vuông tại A và A’ có AB = A’B’, AC > A’C’. Không sử dụng định lý Pitago, chứng minh rằng BC > B’C’.
b) Hai tam giác ABC, A’B’C’ vuông tại A và A’ có AB = A’B’, BC > B’C’.
sử dụng định lý Pytago, chứng minh rằng AC > A’C’
Giải
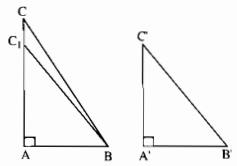
a) Do AC > A’C’ nên lấy được điểm \({C_1}\) trên cạnh AC sao cho \({\rm{A}}{C_1} = A’C’\). Ta có tam giác vuông \(AB{C_1}\) bằng tam giác vuông A’B’C’, suy ra \(B’C’ = B{C_1}\). Mặt khác hai đường xiên BC và \(B{C_1}\) kẻ từ B đến đường thẳng AC lần lượt có hình chiếu trên AC là AC và \({\rm{A}}{C_1}\). Vì \({\rm{A}}C > A{C_1}\) nên \(BC > B{C_1}\). Suy ra BC > B’C’.
b) Dùng phản chứng:
- Giả sử AC < A’C’. Khi đó theo chứng minh câu a) ta có BC < B’C’. Điều này không đúng với giả thiết BC > B’C’.
Giả sử AC = A’C’. Khi đó ta có ∆ABC = ∆A’B’C’ (c.g.c). Suy ra BC = B’C’.
Điều này cũng không đúng với giả thiết BC > B’C’. Vậy ta phải có AC > A’C’.
(Nếu sử dụng định lý Pytago thì có thể giải bài toán sau)
Trong tam giác vuông ABC có \(B{C^2} = A{B^2} + A{C^2}\) (1)
Trong tam giác vuông A’B’C’ có \(B’C{‘^2} = A’B{‘^2} + A’C{‘^2}\) (2)
Theo giả thiết AB = A’B’ nên từ (1) và (2) ta có:
- Nếu AC > A’C’ thì \({\rm{A}}{C^2} > A’C{‘^2}\), suy ra \(B{C^2} > B’C{‘^2}\) hay BC > B’C’
- Nếu BC > B’C’ thì \(B{C^2} > B’C{‘^2}\), suy ra \({\rm{A}}{C^2} > A’C{‘^2}\) hay AC > A’C’
