a) Vẽ đường tròn tâm O bán kính 2cm.
b) Vẽ góc AOB có số đo bằng \(60^\circ \). Hai điểm A, B nằm trên đường tròn (O; 2cm).
c) Vẽ góc BOC có số đo bằng \(60^\circ \). Điểm C thuộc đường tròn (O; 2cm).
d) Vẽ các tía OA’, OB’, OC’ lần lượt là tia đối của các tia OA, OB, OC. Các điểm A’; B’; C’ thuộc đường tròn (O; 2cm).
e) Viết tên năm cặp góc đối đỉnh.
g) Viết tên năm cặp góc bằng nhau mà không đối đỉnh.

a, b, c, d. Hình vẽ:
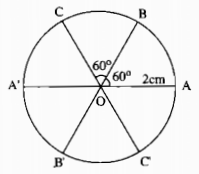
Advertisements (Quảng cáo)
e) Tên 5 cặp góc đối đỉnh:
\(\widehat {AOB}\) và \(\widehat {A’OB’}\); \(\widehat {BOC}\) và \(\widehat {B’OC’}\);
\(\widehat {AOC}\) và \(\widehat {A’OC’}\); \(\widehat {AOB’}\) và \(\widehat {BOA’}\);
\(\widehat {AOC’}\) và \(\widehat {A’OC}\)
g) Vì \(\widehat {AOB} + \widehat {BOC} + \widehat {COA} = 180^\circ \) (Kề bù)
\( \Rightarrow \widehat {COA’} = 180^\circ - 60^\circ - 60^\circ = 60^\circ \)
Tên 5 cặp góc bằng nhau không đối đỉnh:
\(\eqalign{
& \widehat {AOB} = \widehat {BOC} = 60^\circ ;\widehat {BOC} + \widehat {COA’} = 60^\circ \cr
& \widehat {AOB} = \widehat {COA’} = 60^\circ ;\widehat {A’OB’} = \widehat {B’OC’} = 60^\circ \cr
& \widehat {AO{\rm{A}}’} = \widehat {BOB’} = 180^\circ \cr} \)
