Trên trục số cho hai điểm A và B biểu diễn hai số hữu tỉ a và b (a > b)
a) Xác định điểm C biểu diễn số hữu tỉ \({{a + b} \over 2}\)
b) Tìm khoảng cách của hai điểm A và C; B và C, từ đó chứng tỏ C là trung điểm của AB.
c) Chứng minh: \(a > {{a + b} \over 2} > b\)
a)
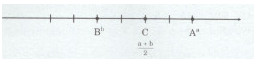
b) \(\eqalign{ & A(a),B(b),C\left( {{{a + b} \over 2}} \right) \cr & AC = \left| {a - {{a + b} \over 2}} \right| = \left| {{{a - b} \over 2}} \right|,BC = \left| {b - {{a + b} \over 2}} \right| = \left| {{{b - a} \over 2}} \right| \cr} \)
Advertisements (Quảng cáo)
Mà \(\left| {{{a - b} \over 2}} \right| = \left| {{{b - a} \over 2}} \right|\) . Nên AC=BC \( \Rightarrow \) C là trung điểm của AB
c)
Vì a > b nên \(a + a > a + b \Rightarrow 2a > a + b \Rightarrow a > {{a + b} \over 2}\)
Mặt khác từ a > b ta có \(a + b > b + b \Rightarrow a + b > 2b \Rightarrow {{a + b} \over 2} > b\)
Vậy \(a > {{a + b} \over 2} > b\)
