1. Đơn thức - Hoạt động 2 trang 59 Tài liệu dạy – học Toán 7 tập 2. Giải bài tập Điền vào ô trống thích hợp :

Điền vào ô trống thích hợp :
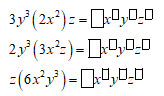
Cả ba đơn thức \(3{y^3}\left( {2{x^2}} \right)z\) , \(2{y^3}\left( {3{x^2}z} \right)\) và \(z\left( {6{x^2}{y^3}} \right)\) đều bằng \(6{x^2}{y^3}z.\) Ta nói \(6{x^2}{y^3}z\) là đơn thức thu gọn của ba đơn thức này với 6 là hệ số, \({x^2}{y^3}z\) là phần biến.
Advertisements (Quảng cáo)

\(\eqalign{ & 3{y^3}\left( {2{x^2}} \right)z = 6{x^2}{y^3}{z^1} \cr & 2{y^3}\left( {3{x^2}z} \right) = 6{x^2}{y^3}{z^1} \cr & z\left( {6{x^2}{y^3}} \right) = 6{x^2}{y^3}{z^1} \cr} \)
