
Thực hành chứng minh định lí 1.
Hãy điền vào chỗ trống (….)
|
GT |
\(\Delta ABC\) |
|
KL |
\(\widehat A + \widehat B + \widehat C = {180^o}\) |
Chứng minh:
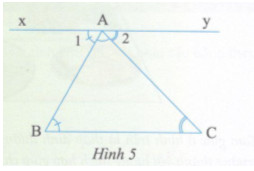
Qua A kẻ đường thẳng xy song song với BC (h.5).
Advertisements (Quảng cáo)
Ta có:
\(\eqalign{ & xy//BC \Rightarrow \widehat B = \widehat {{A_1}}\,\left( {.....} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right) \cr & xy//BC \Rightarrow \widehat C = .....\left( {so\,\,le\,\,trong} \right)\,\,\,\,\,\,\left( 2 \right) \cr} \)
Từ (1) và (2) suy ra:
\(\widehat B + \widehat {BAC} + \widehat C = \widehat A + \widehat {BAC} + \widehat {{A_2}} = \widehat {xAy} = .....\)

Qua A kẻ đường thẳng xy song song với BC (h.5).
Ta có:
\(\eqalign{ & xy//BC \Rightarrow \widehat B = \widehat {{A_1}}\,\left( {so\,\,le\,\,trong} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right) \cr & xy//BC \Rightarrow \widehat C = \widehat {{A_2}}\left( {so\,\,le\,\,trong} \right)\,\,\,\,\,\,\left( 2 \right) \cr} \)
Từ (1) và (2) suy ra:
\(\widehat B + \widehat {BAC} + \widehat C = \widehat A + \widehat {BAC} + \widehat {{A_2}} = \widehat {xAy} = {180^0}\)
