
Điền vào chỗ trống để hoàn thành phần chứng minh định lí đảo.
Chứng minh:
Xét hai trường hợp:
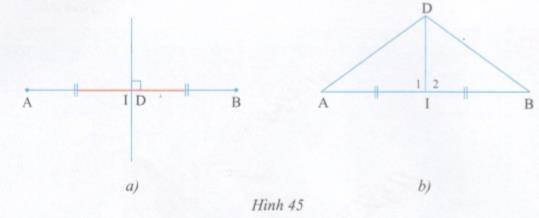
* \(D \in AB\) (hình 45a): Vì DA = DB (gt)
Nên D là………….của đoạn thẳng AB, do đó D thuộc…………của đoạn thẳng AB.
* \(D \notin AB\)(hình 45b): Kẻ đoạn thẳng nối D với trung điểm I của đoạn thẳng AB.
Ta có \(\Delta DAI = \Delta DBI\,\,\left( {c.c.c} \right)\)
Suy ra \(\widehat {{I_1}} = ...........\)
Mặt khác: \(\widehat {{I_1}} + \widehat {{I_2}} = {180^o}\,\,\left( {........} \right)\)
Advertisements (Quảng cáo)
Nên ……………..=………….= 90o
Vậy………..là đường trung trực của đoạn thẳng AB.

Chứng minh:
* \(D \in AB\) (hình 45a). Vì DA = DB (gt)
Nên D là trung điểm của đoạn thẳng AB, do đó D thuộc đường trung trực của đoạn thẳng AB.
* \(D \notin AB\) (hình 45b). Kẻ đoạn thẳng nối D với trung điểm của đoạn thẳng AB.
Ta có \(\Delta DAI = \Delta DBI\,\,\left( {c.c.c} \right)\) \( \Rightarrow {\widehat I_1} = {\widehat I_2}.\)
Mặt khác: \({\widehat I_1} + {\widehat I_2} = {180^o}\) (hai góc kề bù). Nên \({\widehat I_1} = {\widehat I_2} = 90^\circ .\)
Vậy DI là đường trung trực của đoạn thẳng AB.
