Giải bài 4 trang 92 SGK Toán 7 tập 2 - Cánh diều - Bài 6. Trường hợp bằng nhau thứ ba của tam giác: góc- cạnh - góc
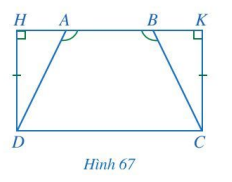
Cho Hình 67 có \(\widehat {AHD} = \widehat {BKC} = 90^\circ ,DH = CK,\widehat {DAB} = \widehat {CBA}\). Chứng minh AD = BC.
Chứng minh tam giác AHD bằng tam giác BKC.
Ta có: \(\widehat {DAB} = \widehat {CBA}\)
Advertisements (Quảng cáo)
Mà \(\widehat {DAB} +\widehat {HAD} =180^0; \widehat {CBA}= \widehat {KBC}\) (2 góc kề bù)
\(\Rightarrow \widehat {HAD} = \widehat {KBC}\)
Mà tổng ba góc trong tam giác bằng 180° và \(\widehat {AHD} = \widehat {BKC} = 90^\circ ,\widehat {HAD} = \widehat {KBC}\) nên \(\widehat {ADH} = \widehat {BCK}\).
Xét tam giác AHD và tam giác BKC có:
\(\widehat {AHD} = \widehat {BKC}\);
HD = KC;
\(\widehat {ADH} = \widehat {BCK}\).
Vậy \(\Delta AHD = \Delta BKC\)(g.c.g) nên AD = BC ( 2 cạnh tương ứng)