![]()
Cho tam giác cân ABC, AB = AC. Lấy điểm M tùy ý nằm giữa B và C (H.9.12).
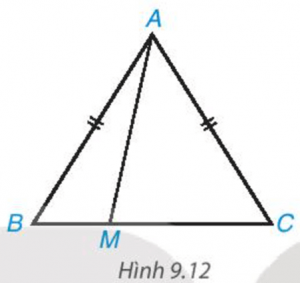
a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M để độ dài AM nhỏ nhất.
b) Chứng minh rằng với mọi điểm M thì AM < AB.
![]()
a)
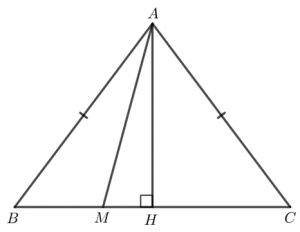
Kẻ AH vuông góc với BC tại H.
M di chuyển trên BC thì AM ≥ AH.
Do đó giá trị nhỏ nhất của AM là AH.
AM = AH khi M trùng H.
Vậy M là chân đường cao kẻ từ A đến BC thì giá trị của AM nhỏ nhất.
Advertisements (Quảng cáo)
b)
+) Khi M trùng H thì AH < AB ( đường vuông góc luôn nhỏ hơn đường xiên)
+) Khi M nằm giữa B và H
Góc AMB là góc ngoài tại đỉnh M của tam giác AHM nên = 90 nên là góc tù nên là góc lớn nhất trong tam giác ABM
Trong tam giác ABM, cạnh AB đối diện với lớn nhất nên cạnh AB lớn nhất (định lí)
AM < AB.
+) Khi M nằm giữa C và H
Góc AMC là góc ngoài tại đỉnh M của tam giác AHM nên = 90 nên là góc tù nên là góc lớn nhất trong tam giác ACM
Trong tam giác ACM, cạnh AC đối diện với lớn nhất nên cạnh AC lớn nhất (định lí)
AM < AC.
Mà AB = AC (gt)
AM < AB
Vậy AM < AB
