Bài 47 trang 127 - Sách giáo khoa Toán 7 tập 1, Bài 47. Trong cách hình 116,117,118 tam giác nào là tam giác cân, tam giác nào là tam giác đều? Vì sao?...

Bài 47. Trong cách hình 116,117,118 tam giác nào là tam giác cân, tam giác nào là tam giác đều? Vì sao?

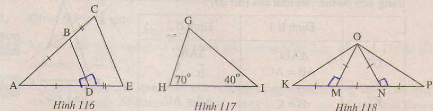
Hình 116.

Ta có: ∆ABD cân vì có AB=AD.

∆ACE cân vì AC=AE(do AB=AD,BC=DE nên AB+BC+AD+DE nên AB + BC= AD+DE hay AC= AE).

Hình 117.

Ta tính được

$\widehat{G}$= 180⁰-($\widehat{H}$+$\widehat{I}$) = 180⁰ - (70⁰+40⁰)=  70⁰

 Nên ∆GHI cân vì($\widehat{G}$=$\widehat{H}$)

Hình 118.

∆OMK là tam giác cân vì OM= MK

∆ONP là tam giác cân vì ON=OP

∆OKP là tam giác cân là vì   $\widehat{K}$=$\widehat{P}$

Suy ra $\widehat{OKM}$+$\widehat{KOM}$=60⁰

mà  $\widehat{OKM}$=$\widehat{KOM}$ nên $\widehat{OKM}$=30⁰

Tương tự $\widehat{OPM}$=30⁰