Bài 55 trang 80 sgk Toán lớp 7- tập 2, Cho hình bên:...

55. Cho hình bên:

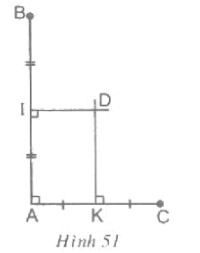
Chứng minh ba điểm B, C, D thẳng hàng

Gợi ý: Chứng minh \(\widehat{ADB}+ \widehat{ADC}\) = 180⁰

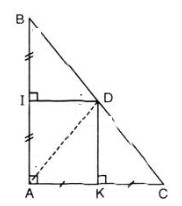
Từ hình vẽ ta có:

DK là trung trực của Ac, DI là đường trung trực của AB. Do đó ∆ADK = ∆CDK (c.c.c)

=> \(\widehat{ADK}= \widehat{CDK}\)

hay DK là phân giác \(\widehat{ADC}\)

=> \(\widehat{ADK}\) = \(\frac{1}{2}\)\(\widehat{ADC}\)

∆ADI = ∆BDI (c.c.c)

=> \(\widehat{ADI}= \widehat{BDI}\)

=> DI là phân giác \(\widehat{ADB}\)

=> \(\widehat{ADI}\) = \(\frac{1}{2}\) \(\widehat{ADB}\)

Vì AC // DI ( cùng vuông góc với AB) mà DK ⊥ AC 

=> DK ⊥ DI

hay \(\widehat{ADK}\) + \(\widehat{ADI}\) = 90⁰

Do đó  \(\frac{1}{2}\)\(\widehat{ADC}\) + \(\frac{1}{2}\) \(\widehat{ADB}\) = 90⁰

=> \(\widehat{ADC}\) + \(\widehat{ADB}\) =  180⁰