
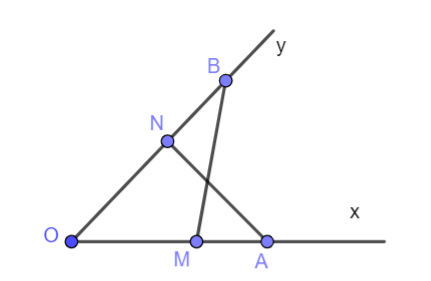
Bài 2 (4.30). Cho góc xOy. Trên tia Ox lấy hai điểm A, M, trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM = ON, OA > OM.Chứng minh rằng:
a) \(\Delta OAN = \Delta OBM\)
b) \(\Delta AMN = \Delta BNM\)

Chứng minh hai tam giác bằng nhau theo trường hợp c – g – c

|
GT |
\(\begin{array}{l}\widehat {xOy};A,M \in Ox;B,N \in Oy\\OA = OB,OM = ON,OA > OM\end{array}\) |
|
KL |
Advertisements (Quảng cáo) a) \(\Delta OAN = \Delta OBM\) b) \(\Delta AMN = \Delta BNM\) |
a) Xét hai tam giác OAN và OBM ta có:
OA = OB (theo giả thiết)
\(\widehat {NOA} = \widehat {xOy} = \widehat {MOB}\)
ON = OM (theo giả thiết)
Vậy \(\Delta OAN = \Delta OBM\)( c – g – c)
b) Xét hai tam giác AMN và BNM ta có:
AN = BM, \(\widehat {MAN} = \widehat {OAN} = \widehat {OBM} = \widehat {NBM}\)(vì \(\Delta OAN = \Delta OBM\))
AM = OA – OM = OB – ON = BN
Vậy \(\Delta AMN = \Delta BNM\)( c – g – c)
