
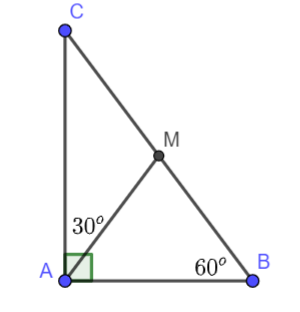
Bài 6 (4.39). Cho tam giác ABC vuông tại A có \(\widehat B = {60^o}\). Trên cạnh BC lấy điểm M sao cho \(\widehat {CAM} = {30^o}\). Chứng minh rằng
a) Tam giác CAM cân tại M
b) Tam giác BAM đều
c) M là trung điểm của đoạn thẳng BC.

Tam giác cân có hai cạnh bằng nhau và hai góc ở đáy bằng nhau
tam giác đều có ba cạnh bằng nhau và ba góc bằng nhau

|
GT |
\(\Delta ABC\)vuôngtại A, \(\widehat B = {60^o}\),\(M \in BC,\widehat {CAM} = {30^o}\) |
|
Advertisements (Quảng cáo) KL |
a) Tam giác CAM cân tại M b) Tam giác BAM đều c) MB = MC. |
a) Do hai góc B và C trong tam giác vuông ABC phụ nhau nên:
\(\widehat {MCA} = \widehat {BCA = }{90^o} - {60^o} = {30^o} = \widehat {CAM}\)
Suy ra \(\Delta AMC\) cân tại M.
b) Ta có:
\(\begin{array}{l}\widehat {BAM} = \widehat {BAC} - \widehat {CAM} = {90^o} - {30^o} = {60^o}\\\widehat {AMB} = {180^o} - \widehat {BAM} - \widehat {ABM} = {60^o}\end{array}\)
Vậy tam giác BAM có ba góc bằng nhau nên nó là tam giác đều.
c) Từ phần a và b ta suy ra MA = MC (\(\Delta AMC\) cân tại M), MA = MB (\(\Delta ABM\) đều). Vì vậy MB = MC hay M là trung điểm BC.
