
Cho tam giác \(ABC\) cân tại \(A\), có \(M\) là trung điểm của \(BC\). Kể tia \(Mx\) song song với \(AC\) cắt \(AB\) tại \(E\) và tia \(My\) song song với \(AB\) cắt \(AC\) tại \(F\). Chứng minh:
a) \(EF\) là đường trung bình của tam giác \(ABC\);
b) \(AM\) là đường trung trực của \(EF\).

Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh tam giác đó.
Advertisements (Quảng cáo)
Tính chất: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh đó.

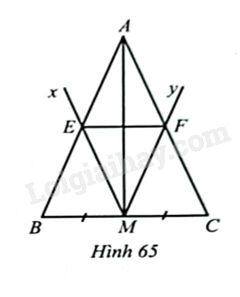
a) Vì \(M\) là trung điểm của \(BC,ME//AC,MF//AB\) nên \(E,F\) lần lượt là trung điểm của \(AB.AC\). Do đó, \(EF\) là đường trung bình của tam giác \(ABC\).
b) Ta có \(AE = \frac{{AB}}{2},AF = \frac{{AC}}{2}\) và \(AB = AC\) suy ra \(AE = AF\) (1). Lại có \(ME,MF\) là các đường trung bình của tam giác \(ABC\) nên \(ME = \frac{{AC}}{2},MF = \frac{{AB}}{2}\). Mà \(AB = AC\) suy ra \(ME = MF\) (2). Từ (1) và (2) suy ra \(AM\) là đường trung trực của \(EF\).
