Để đo khoảng cách \(AB\), trong đó điểm \(B\) không tới được, người ta tiến hành đo bằng cách lấy các điểm \(C,D,E\) sao cho \(AD=10\)m, \(CD=7\)m, \(DE=4\)m (Hình 57). Khi đó, khoảng cách \(AB\) (tính theo đơn vị mét và làm tròn kết quả đến hàng phần mười) là: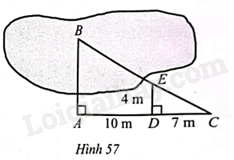 
A. 9,3 mB. 9,4 mC. 9,6 mD. 9,7 m 
Áp dụng trường hợp đồng dạng thứ nhất của tam giác vào tam giác vuông:
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
Chọn đáp án D
Advertisements (Quảng cáo)
Xét hai tam giác \(\Delta ABC\) và \(\Delta DEC\) có
\(\widehat{BAC}=\widehat{EDC};\widehat{ACB}=\widehat{DCE}\)
\(=>\Delta ABC\backsim \Delta DEC\) (g.g)
\(=>\frac{AB}{DE}=\frac{AC}{DC}\)
Hay \(\frac{AB}{4}=\frac{10+7}{7}=>AB=\frac{4.\left( 10+7 \right)}{7}=9,7\left( m \right)\)
Vậy \(AB=9,7\) (m).