Bài 66 trang 84 SBT Toán 8 – Cánh diều: Cho điểm $M$ thuộc đoạn thẳng $AB$, với $MA=a, MB=b$...

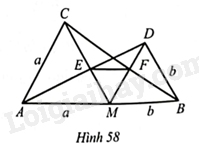
Cho điểm $M$ thuộc đoạn thẳng $AB$, với $MA=a,MB=b$. Vẽ hai tam giác đều $AMC$ và $BMD$; gọi $E$ là giao điểm của $AD$ và $CM$, $F$ là giao điểm của $DM$ và $BC$ (Hình 58).

a) Chứng minh $EF//AB$

b) Tính $ME,MF$ theo $a,b$.

Tam giác $A’B’C’$ gọi là đồng dạng với tam giác $ABC$ nếu:

$\widehat{A’}=\widehat{A},\widehat{B’}=\widehat{B},\widehat{C’}=\widehat{C}$ ; $\frac{A’B’}{AB}=\frac{B’C’}{BC}=\frac{A’C’}{AC}$.

Kí hiệu là $\Delta A’B’C’\backsim \Delta ABC$.

Tỉ số các cạnh tương ứng $\frac{A’B’}{AB}=\frac{B’C’}{BC}=\frac{C’A’}{CA}=k$ gọi là tỉ số đồng dạng.

a) Ta có $\widehat{DMB}=\widehat{CAM}=60{}^\circ$, $\widehat{DBM}=\widehat{CMA}=60{}^\circ$. Suy ra $MD//AC,DB//CM$.

Do $MD//AC$ nên $\frac{EC}{EM}=\frac{AC}{DM}=\frac{a}{b}$ (theo định lí Thales)

Tương tự, do $DB//CM$ nên $\frac{CF}{FB}=\frac{CM}{DB}=\frac{a}{b}$

Từ đó, ta có: $\frac{EC}{EM}=\frac{CF}{FB}=\frac{a}{b}$ nên $EF//MB$ hay $EF//AB$

b) Từ $EF//AB$ suy ra tam giác $EMF$ là tam giác đều.

Từ đó, ta có: $\frac{EC=\frac{a}{a+b}}{CM}=\frac{EF}{MB}=\frac{EC+EF}{CM+MB}$

$=>EF=\frac{ab}{a+b}$

Vì tam giác $MEF$ là tam giác đều nên $ME=MF=EF=\frac{ab}{a+b}$.