
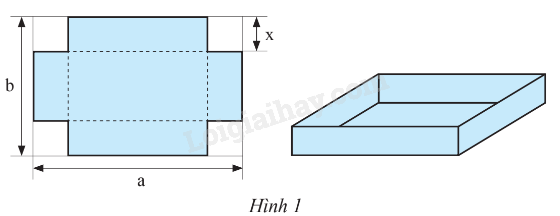
Từ một tấm tôn hình chữ nhật có chiều dài bằng a (cm), chiều rộng bằng b (cm), người ta cắt bỏ bốn hình vuông cạnh bằng x (cm) ở bốn góc, rồi gấp và hàn thành thùng không có nắp (Hình 1). Viết biểu thức biểu thị:
a) Thể tích nước tối đa mà thùng có thể chứa được.
b) Tổng diện tích của năm mặt của chiếc thùng.

+ Sử dụng kiến thức nhân đơn thức với đa thức: Để nhân đơn thức với đa thức ta nhân đơn thức đó với từng hạng tử của đa thức, rồi cộng các kết quả với nhau.
+ Sử dụng kiến thức cộng trừ hai đa thức để tính:
- Viết hai đa thức trong ngoặc nối với nhau bằng dấu cộng (+) hay trừ (–).
- Bỏ dấu ngoặc rồi thu gọn đa thức thu được.
+ Sử dụng kiến thức nhân hai đa thức để tính: Để nhân hai đa thức, ta lấy từng hạng tử của đa thức này nhân với đa thức kia, rồi cộng các kết quả với nhau.

Thùng trên có chiều dài là: \(a - 2x\left( {cm} \right)\), chiều rộng là \(b - 2x\left( {cm} \right)\), chiều cao là x (cm)
Advertisements (Quảng cáo)
a) Thể tích của thùng là:
\(V = \left( {a - 2x} \right)\left( {b - 2x} \right)x = \left[ {a\left( {b - 2x} \right) - 2x\left( {b - 2x} \right)} \right]x\)
\( = \left( {ab - 2ax - 2bx + 4{x^2}} \right)x = abx - 2a{x^2} - 2b{x^2} + 4{x^3}\)
Vậy thể tích nước tối đa mà thùng có thể chứa được là \(abx - 2a{x^2} - 2b{x^2} + 4{x^3}\left( {c{m^3}} \right)\)
b) Tổng diện tích năm mặt của chiếc thùng là:
\(S = \left( {a - 2x} \right)\left( {b - 2x} \right) + 2x\left( {a - 2x} \right) + 2x\left( {b - 2x} \right)\)
\( = a\left( {b - 2x} \right) - 2x\left( {b - 2x} \right) + 2ax - 4{x^2} + 2bx - 4{x^2}\)
\( = ab - 2ax - 2bx + 4{x^2} + 2ax - 4{x^2} + 2bx - 4{x^2}\)
\( = ab + \left( {2ax - 2ax} \right) + \left( {2bx - 2bx} \right) + \left( {4{x^2} - 4{x^2} - 4{x^2}} \right) = ab - 4{x^2}\)
Vậy tổng diện tích của năm mặt của chiếc thùng là \(ab - 4{x^2}\left( {c{m^2}} \right)\)
