Sử dụng kiến thức về trường hợp đồng dạng thứ ba của hai tam giác (g.g) để tính. Gợi ý giải bài 10 trang 64 sách bài tập toán 8 - Chân trời sáng tạo tập 2 - Bài 2. Các trường hợp đồng dạng của hai tam giác. Trong Hình 10, cho biết \(AB = 4, 2, IA = 6, IC = 10, \widehat {ABI} = {60^0}\), \(\widehat {CDx} = {120^0}\)....
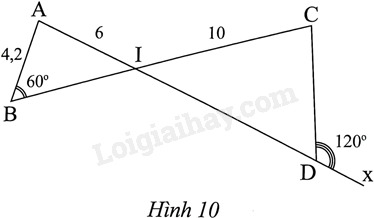
Trong Hình 10, cho biết \(AB = 4,2,IA = 6,IC = 10,\widehat {ABI} = {60^0}\), \(\widehat {CDx} = {120^0}\). Tính độ dài CD.
Sử dụng kiến thức về trường hợp đồng dạng thứ ba của hai tam giác (g.g) để tính: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Advertisements (Quảng cáo)
Ta có: \(\widehat {CDI} = {180^0} - \widehat {CDx} = {60^0}\)
Tam giác ABI và tam giác CDI có: \(\widehat B = \widehat {CDI}\left( { = {{60}^0}} \right),\widehat {AIB} = \widehat {CID}\) (hai góc đối đỉnh)
Do đó, $\Delta ABI\backsim \Delta CDI\left( g.g \right)$. Suy ra: \(\frac{{AB}}{{CD}} = \frac{{AI}}{{CI}}\), hay \(\frac{{4,2}}{{CD}} = \frac{6}{{10}}\), suy ra \(CD = \frac{{4,2.10}}{6} = 7\)