Bài 11 trang 64 SBT Toán 8 - Chân trời sáng tạo tập 2: Quan sát Hình 1Vẽ vào tờ giấy tam giác MNP với $NP = 6cm, \widehat N = {45^0}, \widehat P = {75^0}$...

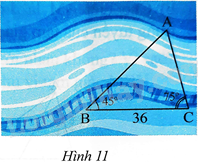
Quan sát Hình 11. Vẽ vào tờ giấy tam giác MNP với $NP = 6cm,\widehat N = {45^0},\widehat P = {75^0}$.

a) Chứng minh $\Delta MNP\backsim \Delta ABC$

b) Dùng thước đo chiều dài cạnh MP của tam giác MNP. Tính khoảng cách giữa hai điểm A và C ở hai bờ sông trong Hình 11.

Sử dụng kiến thức về trường hợp đồng dạng thứ ba của hai tam giác (g.g): Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.

a) Tam giác MNP và tam giác ABC có: $\widehat N = \widehat B\left( { = {{45}^0}} \right),\widehat P = \widehat C\left( { = {{75}^0}} \right)$

Do đó, $\Delta MNP\backsim \Delta ABC\left( g.g \right)$

b) Vì $\Delta MNP\backsim \Delta ABC\left( cmt \right)$ nên $\frac{{MP}}{{AC}} = \frac{{NP}}{{BC}}$, do đó, $AC = \frac{{MP.BC}}{{NP}} = \frac{{MP.36}}{6} = 6MP$

Học sinh đo độ dài đọan thẳng MP trong hình mình vẽ, từ đó tính được AC.