
Cho tứ giác ABCD như Hình 12.
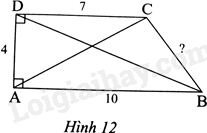
a) Tính độ dài hai đường chéo và cạnh còn lại của tứ giác ABCD.
b) Cho biết góc B bằng \({53^0}\). Tìm số đo góc C.

a) Sử dụng kiến thức về định lí Pythagore vào tam giác vuông để tính: Trong một tam giác vuông, bình vuông độ dài của cạnh huyền bằng tổng các bình phương độ dài của hai cạnh góc vuông.
b) Sử dụng kiến thức về tổng các góc của một tứ giác để tính góc C: Tổng số đo các góc của một tứ giác bằng 360 độ.

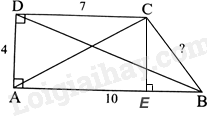
a) Áp dụng định lí Pythagore vào tam giác ADC vuông tại D có:
\(A{C^2} = A{D^2} + D{C^2} = {4^2} + {7^2} = 65\), suy ra \(AC = \sqrt {65} \)
Áp dụng định lí Pythagore vào tam giác ADB vuông tại A có:
Advertisements (Quảng cáo)
\(B{D^2} = A{D^2} + A{B^2} = {4^2} + {10^2} = 116\), suy ra \(BD = \sqrt {116} \)
Kẻ CE \( \bot \) AB. Do AD \( \bot \) AB suy ra CE // AD.
Suy ra \(\widehat {DAC} = \widehat {ACE}\) (hai góc so le trong)
Xét \(\Delta ADC\) và \(\Delta CEA\) có:
\(\widehat D = \widehat E = {90^o}\)
\(\widehat {DAC} = \widehat {ACE}\)(cmt)
AC chung
=> \(\Delta ADC\) = \(\Delta CEA\) (cạnh huyền – góc nhọn)
=> AD = CE = 4, DC = AE = 7 (các cặp cạnh tương ứng)
Ta có AE + EB = AB => EB = AB – AE = 10 – 7 = 3
Áp dụng định lí Pythagore vào tam giác CEB vuông tại E, ta có:
\(C{E^2} + E{B^2} = {4^2} + {3^2} = 25 = {5^2} = B{C^2}\), suy ra BC = 5
b) Tứ giác ABCD có: \(\widehat {DCB} = {360^0} - \widehat {DAB} - \widehat {ADC} - \widehat {ABC} = {360^0} - {90^0} - {90^0} - {53^0} = {127^0}\)
