
Cho tam giác đều ABC, từ B và C kẻ các đường thẳng song song với AC và AB, hai đường thẳng này cắt nhau tại M. Qua M kẻ đường thẳng cắt AB tại E và cắt AC tại F. Chứng minh rằng:
a) \(\frac{{CA}}{{CF}} = \frac{{ME}}{{MF}}\) và \(\frac{{BE}}{{BA}} = \frac{{ME}}{{MF}}\).
b) $\Delta BCE\backsim \Delta CFB$.

Sử dụng kiến thức về trường hợp đồng dạng thứ hai của hai tam giác (c.g.c) để tính chứng minh: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đó đồng dạng với nhau.

Advertisements (Quảng cáo)
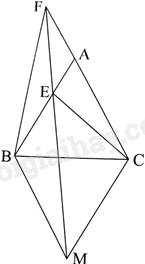
a) Tam giác FCM có AE//CM nên theo định lí Thalès ta có: \(\frac{{CA}}{{CF}} = \frac{{ME}}{{MF}}\)
Tam giác FAE có AF//BM nên theo hệ quả định lí Thalès ta có: \(\frac{{AE}}{{BE}} = \frac{{EF}}{{ME}}\)
Ta có: \(\frac{{AE}}{{BE}} + \frac{{BE}}{{BE}} = \frac{{EF}}{{ME}} + \frac{{ME}}{{ME}}\), suy ra \(\frac{{BA}}{{BE}} = \frac{{MF}}{{ME}}\) hay \(\frac{{BE}}{{BA}} = \frac{{ME}}{{MF}}\)
b) Ta có: \(\frac{{CA}}{{CF}} = \frac{{BE}}{{BA}}\left( { = \frac{{ME}}{{MF}}} \right)\), mà \(AB = AC = BC\)
Do đó, \(\frac{{BC}}{{CF}} = \frac{{BE}}{{CB}}\), lại có: \(\widehat {EBC} = \widehat {BCF}\) (do tam giác ABC đều) nên $\Delta BCE\backsim \Delta CFB\left( c.g.c \right)$
