
Hai đường trung tuyến BM, CN của tam giác ABC cân tại A cắt nhau tại G. Gọi H, K lần lượt là điểm sao cho trung điểm của GH là M, trung điểm của GK là N. Chứng minh tứ giác BCHK là hình chữ nhật.

Sử dụng kiến thức về dấu hiệu nhận biết hình chữ nhật để chứng minh: Hình bình hành có một góc vuông là hình chữ nhật.

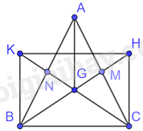
Vì BM, CN là hai đường trung tuyến của tam giác ABC nên M, N lần lượt là trung điểm của AC, AB. Hai đường trung tuyến này cắt nhau tại G nên G là trọng tâm của tam giác ABC. Do đó, AG là đường trung tuyến của tam giác.
Advertisements (Quảng cáo)
Mà tam giác ABC cân tại A nên AG là đường trung tuyến đồng thời là đường cao. Suy ra \(AG \bot BC\)
Do M là trung điểm của AC và GH nên tứ giác AGCH là hình bình hành, do đó \(HC = AG\), HC//AG
Do N là trung điểm của AB và KG nên tứ giác AKBG là hình bình hành, do đó \(KB = AG,\) KB//AG
Do đó, \(HC = KB,HC//KB\)
Suy ra, tứ giác KBCH là hình bình hành.
Vì \(AG \bot BC\) nên \(KB \bot BC\) nên \(\widehat {KBC} = {90^0}\)
Vậy tứ giác BCHK là hình chữ nhật.
