
Khái niệm tam giác, tứ giác có thể mở rộng thành khái niệm n – giác (n là số tự nhiên lớn hơn 2) như sau:
n – giác là hình tạo bởi n đoạn thẳng (gọi là cạnh của n – giác) \({A_0}{A_1},{A_1}{A_2},...,{A_{n - 1}}{A_n},{A_n}{A_0}\) (các điểm \({A_0},{A_1},...,{A_n}\) gọi là đỉnh của n – giác), trong đó không có ba đỉnh nào cùng nằm trên một đường thẳng và hình nằm về một phía đối với mỗi đường thẳng chứa một cạnh.
Khi \(n = 3;4;5;6;7;8,\) n – giác còn được gọi lần lượt là tam giác, tứ giác, ngũ giác, lục giác, thất giác, bát giác.
Hai đỉnh của n – giác gọi là kề nhau nếu chúng là hai đỉnh của một cạnh của n – giác.
Đoạn thẳng nối hai đỉnh không kề nhau của n – giác gọi là một đường chéo của n – giác.
a) Chứng minh qua mỗi đỉnh của n – giác, có \(n - 3\) đường chéo của n – giác. Từ đó suy ra n – giác có \(\frac{{n\left( {n - 3} \right)}}{2}\) đường chéo.
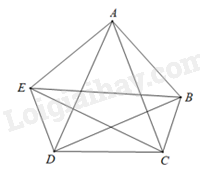
b) Hãy vẽ tất cả các đường chéo của một ngũ giác \(\left( {n = 5} \right)\)
Advertisements (Quảng cáo)

Sử dụng kiến thức về đường chéo của đa giác để chứng minh: Đoạn thẳng nối hai đỉnh không kề nhau của n – giác gọi là một đường chéo của n – giác.

a) Không có đường chéo nào của n – giác nối một đỉnh cho trước với chính đỉnh đó và với hai đỉnh kề với đỉnh đó nên có \(n - 3\) đường chéo của n – giác qua đỉnh đang xét.
Tính theo cách đó thì n – giác có \(n\left( {n - 3} \right)\) đường chéo, nhưng mỗi đường chéo được tính hai lần nên n – giác có tất cả \(\frac{{n\left( {n - 3} \right)}}{2}\) đường chéo.
b) Giả sử ta có ngũ giác ABCDE, khi đó ngũ giác này có \(\frac{{5\left( {5 - 3} \right)}}{2} = 5\) đường chéo, đó là: AC, AD, BD, BE, CE.
