
Cho tam giác ABC. Với mỗi điểm M nằm giữa B và C, lấy điểm N thuộc cạnh AB, điểm P thuộc cạnh AC sao cho MN//AC, MP//AB.
a) Tứ giác ANMP là hình gì?
b) Hỏi M là vị trí nào để tứ giác ANMP là một hình thoi?
c) Tam giác ABC phải thỏa mãn điều kiện gì để tứ giác ANMP là một hình chữ nhật?
d) Khi tam giác ABC thỏa mãn điều kiện nói trong câu c, tìm vị trí của M để NP ngắn nhất.
e) Tam giác ABC thỏa mãn điều kiện gì và M ở vị trí nào trên cạnh BC để tứ giác ANMP là một hình vuông?

a) Sử dụng kiến thức dấu hiệu nhận biết hình bình hành để chứng minh: Tứ giác có các cặp cạnh đối song song là hình bình hành.
b) Sử dụng kiến thức dấu hiệu nhận biết hình thoi để chứng minh: Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
c) Sử dụng kiến thức dấu hiệu nhận biết hình chữ nhật để chứng minh: Hình bình hành có một một góc vuông là hình chữ nhật.
Advertisements (Quảng cáo)
d) Sử dụng kiến thức tính chất hình chữ nhật để chứng minh: Hình chữ nhật có hai đường chéo bằng nhau.
e) Sử dụng kiến thức hình vuông để chứng minh: Hình vuông vừa là hình chữ nhật vừa là hình thoi.

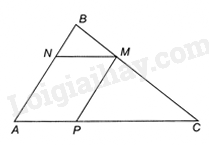
a) Tứ giác ANMP có: MN//AP, MP//AN nên tứ giác ANMP là hình bình hành.
b) Để hình bình hành ANMP là hình thoi thì AM là tia phân giác của góc BAC. Khi đó, M là giao điểm của tia phân giác góc BAC và cạnh BC.
c) Để hình bình hành ANMP là hình chữ nhật thì \(\widehat {NAP} = {90^0}\) hay \(\widehat {BAC} = {90^0}\), suy ra tam giác ABC vuông tại A.
d) Khi tam giác ABC vuông tại A, ANMP là hình chữ nhật thì \(AM = NP\)
Vậy NP ngắn nhất khi AM ngắn nhất, suy ra AM là đường cao của tam giác ABC.
e) Tứ giác ANMP là hình vuông thì tứ giác ANMP vừa là hình thoi vừa là hình vuông.
Theo phần a và phần b thì tam giác ABC vuông tại A và AM là tia phân giác của góc BAC.
