
Xét tam giác ABC vuông cân tại A. Lấy trên cạnh BC hai điểm D, E sao cho \(BD = DE = EC\). Lấy các điểm F, G lần lượt thuộc cạnh AC, AB sao cho FE, GD vuông góc với BC. Chứng minh tứ giác DEFG là một hình vuông.

Sử dụng dấu hiệu nhận biết hình vuông để chứng minh: Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

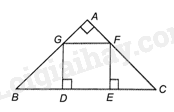
Vì \(\Delta \)ABC vuông cân tại A nên \(\widehat B = \widehat C = {45^0}\), \(AB = AC\)
Vì \(GD \bot BC\) nên \(\widehat {GDB} = \widehat {GDE} = {90^0}\)
Vì \(FE \bot BC\) nên \(\widehat {FED} = \widehat {FEC} = {90^0}\)
Tam giác BDG có: \(\widehat {GDB} = {90^0},\widehat B = {45^0}\) nên tam giác GBD vuông cân tại D, do đó, \(\widehat {BGD} = {45^0}\) và \(BD = GD\)
Mà \(BD = DE\) nên \(GD = DE\)
Advertisements (Quảng cáo)
Tam giác GBD và tam giác FCE có:
\(\widehat {GDB} = \widehat {FEC} = {90^0},\widehat B = \widehat C = {45^0},BD = EC\)
Do đó, \(\Delta GDB = \Delta FEC\left( {cgv - gn} \right)\), suy ra \(BG = FC\)
Mà \(AB = AC\) (cmt) nên \(AB - BG = AC - FC\), suy ra \(GA = FA\)
Tam giác GAF vuông tại A có \(GA = FA\) nên tam giác GAF vuông cân tại A. Do đó, \(\widehat {FGA} = {45^0}\)
Ta có: \(\widehat {FGA} + \widehat {FGD} + \widehat {DGB} = {180^0}\)
\({45^0} + \widehat {FGD} + {45^0} = {180^0}\), suy ra \(\widehat {FGD} = {90^0}\)
Tứ giác GDEF có: \(\widehat {GDE} + \widehat {FED} + \widehat {FGD} + \widehat {GFE} = {360^0}\)
Nên \(\widehat {GFE} = {90^0}\)
Tứ giác DEFG có: \(\widehat {GDE} = \widehat {FED} = \widehat {FGD} = \widehat {GFE} = {90^0}\) nên DEFG là hình chữ nhật, mà \(GD = DE\) nên DEFG là hình vuông.
