
Cho \(\Delta ABC\) có AD, BE, CF lần lượt là đường phân giác của góc A, góc B, góc C \(\left( {D \in BC,E \in AC,F \in AB} \right)\). Chứng minh rằng \(\frac{{AE}}{{EC}}.\frac{{CD}}{{DB}}.\frac{{BF}}{{FA}} = 1\).

Sử dụng kiến thức về tính chất đường phân giác của tam giác để chứng minh: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn thẳng ấy.

Advertisements (Quảng cáo)
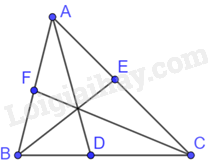
Vì AD là tia phân giác của góc BAC trong tam giác ABC nên \(\frac{{CD}}{{DB}} = \frac{{AC}}{{AB}}\) (tính chất đường phân giác của tam giác)
Vì BE là tia phân giác của góc ABC trong tam giác ABC nên \(\frac{{AE}}{{EC}} = \frac{{AB}}{{BC}}\) (tính chất đường phân giác của tam giác)
Vì CF là tia phân giác của góc BCA trong tam giác ABC nên \(\frac{{BF}}{{FA}} = \frac{{BC}}{{AC}}\) (tính chất đường phân giác của tam giác)
Do đó, \(\frac{{AE}}{{EC}}.\frac{{CD}}{{DB}}.\frac{{BF}}{{FA}} = \frac{{AB}}{{BC}}.\frac{{AC}}{{AB}}.\frac{{BC}}{{AC}} = 1\)
