
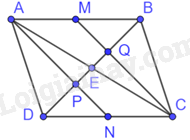
Cho hình bình hành ABCD có M, N lần lượt là trung điểm AB và CD. Gọi P, Q theo thứ tự là giao điểm của AN và CM với đường chéo BD. Chứng minh rằng: \(DP = PQ = QB\)

Sử dụng kiến thức tỉ số đoạn thẳng để chứng minh: Hai đoạn thẳng AB và CD tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức: \(\frac{{AB}}{{CD}} = \frac{{A’B’}}{{C’D’}}\) hay \(\frac{{AB}}{{A’B’}} = \frac{{CD}}{{C’D’}}\).

Advertisements (Quảng cáo)
Gọi E là giao điểm của AC và BD trong hình bình hành ABCD nên \(DE = BE = \frac{1}{2}BD\), \(AE = EC = \frac{1}{2}AC\)
Tam giác ADC có hai đường trung tuyến AN và DE cắt nhau tại P nên P là trọng tâm của tam giác ADC. Do đó, \(DP = \frac{2}{3}DE = \frac{1}{3}BD\).
Tam giác ABC có hai đường trung tuyến BE và CM cắt nhau tại Q nên Q là trọng tâm của tam giác ABC. Do đó, \(BQ = \frac{2}{3}BE = \frac{1}{3}BD\).
Do đó, \(BQ = DP = \frac{1}{3}BD\)
Mà \(BQ + DP + PQ = BD\) nên \(PQ = \frac{1}{3}BD\)
Vậy \(DP = PQ = QB\)
