
Giá trị sổ sách là giá trị của tài sản mà một công ty sử dụng để tạo ra bảng cân đối kế toán của mình. Một số công ty khấu hao tài sản của họ bằng cách sử dụng phương pháp khấu hao đường thẳng để giá trị của tài sản giảm đi một lượng cố định mỗi năm. Mức suy giảm phụ thuộc vào thời gian sử dụng hữu ích mà công ty đặt vào tài sản. Giả sử rằng một công ty vận tải vừa mua một số ô tô mới với giá 640 triệu đồng một chiếc. Công ty lựa chọn khấu hao từng chiếc xe theo phương pháp khấu hao đường thẳng trong vòng 8 năm. Điều này có nghĩa là sau mỗi năm, mỗi chiếc xe giảm giá \(640:8 = 80\) triệu đồng.

a) Tìm hàm số bậc nhất biểu thị giá trị số sách V (tính theo triệu đồng) của mỗi chiếc ô tô theo tuổi x (năm) của nó.
b) Vẽ đồ thị hàm số bậc nhất tìm được ở câu a.
c) Giá trị sổ sách của mỗi chiếc xe sau 3 năm là bao nhiêu?
d) Khi nào giá trị sổ sách của mỗi chiếc xe là 160 triệu đồng?

a) Sử dụng khái niệm hàm số bậc nhất để tìm hàm số: Hàm số bậc nhất là hàm số cho bởi công thức \(y = ax + b,\) trong đó a, b là các số cho trước và \(a \ne 0\)
b) Sử dụng kiến thức về cách vẽ đồ thị hàm số bậc nhất \(y = ax + b\left( {a \ne 0} \right)\) để vẽ các đồ thị
+ Khi \(b = 0\) thì \(y = ax\). Đồ thị của hàm số \(y = ax\) là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm A(1; a)
+ Khi \(b \ne 0\), ta thường xác định hai điểm đặc biệt trên đồ thị là giao điểm của đồ thị với hai trục tọa độ như sau:
- Cho \(x = 0\) thì \(y = b\), ta được điểm P(0; b) thuộc trục tung Oy.
Advertisements (Quảng cáo)
- Cho \(y = 0\) thì \(x = \frac{{ - b}}{a}\), ta được điểm \(Q\left( { - \frac{b}{a};0} \right)\) thuộc trục hoành Ox.
- Vẽ đường thẳng đi qua hai điểm P, Q ta được đồ thị của hàm số \(y = ax + b\)
c, d) Sử dụng giá trị của hàm số để tính: Cho hàm số \(y = f\left( x \right)\), nếu ứng với \(x = a\) ta có\(y = f\left( a \right)\) thì f(a) được gọi là giá trị của hàm số \(y = f\left( x \right)\) tại \(x = a\).

a) Hàm số bậc nhất biểu thị giá trị số sách V (tính theo triệu đồng) của mỗi chiếc ô tô theo tuổi x (năm) của nó là: \(V = 640 - 80x = - 80x + 640\) (triệu đồng)
b) Đồ thị hàm số \(y = V = - 80x + 640\) đi qua 2 điểm \(\left( {0;640} \right)\) và \(\left( {8;0} \right)\)
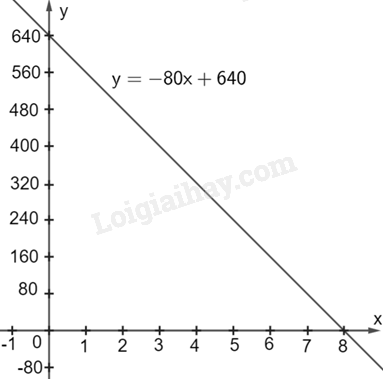
c) Với \(x = 3\) ta có: \(V = - 80.3 + 640 = 400\) (triệu đồng)
d) Với \(V = 160\) ta có: \(160 = - 80x + 640\)
\(80x = 480\)
\(x = 6\)
Vậy sau 6 năm thì giá trị sổ sách của mỗi chiếc xe là 160 triệu đồng.
