
Cho tam giác ABC và hai điểm M, N lần lượt nằm trên AB, AC sao cho MN song song với BC. Gọi ME, BF lần lượt là phân giác của các góc M, B của các tam giác AMN và tam giác ABC. Chứng minh rằng:
a) $\Delta MEN\backsim \Delta BFC$
b) \(\frac{{AE}}{{AF}} = \frac{{MN}}{{BC}}\)

a) Sử dụng kiến thức về định lý (trường hợp đồng dạng góc – góc) để chứng minh hai tam giác đồng dạng: Nếu hai góc của tam giác lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
b) + Sử dụng kiến thức hệ quả định lý Thalès: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
+ Sử dụng tính chất đường phân giác của tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy.

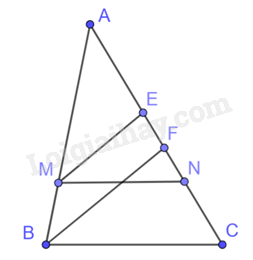
a) Vì MN//BC (gt) nên
Advertisements (Quảng cáo)
+ \(\widehat {ENM} = \widehat C\) (hai góc đồng vị)
+ \(\widehat {AMN} = \widehat {ABC}\) (hai góc đồng vị)
Mà ME, BF lần lượt là phân giác của các góc M, B của các tam giác AMN và tam giác ABC nên \(\widehat {EMN} = \frac{1}{2}\widehat {AMN} = \frac{1}{2}\widehat {ABC} = \widehat {FBC}\)
Tam giác MEN và tam giác BFC có:
\(\widehat {ENM} = \widehat C\) (cmt), \(\widehat {EMN} = \widehat {FBC}\) (cmt)
Do đó, $\Delta MEN\backsim \Delta BFC\left( g-g \right)$
b) Tam giác ABC có: MN//BC nên theo hệ quả định lý Thalès ta có: \(\frac{{MN}}{{BC}} = \frac{{AM}}{{AB}}\) (1)
Vì ME, BF lần lượt là phân giác của các góc M, B của các tam giác AMN và tam giác ABC nên \(\widehat {EMA} = \frac{1}{2}\widehat {AMN} = \frac{1}{2}\widehat {ABC} = \widehat {FBA}\)
Do đó, \(\widehat {EMA} = \widehat {FBA}\), mà hai góc này ở vị trí đồng vị nên ME//BF.
Tam giác ABF có: ME//BF nên theo hệ quả định lý Thalès ta có: \(\frac{{AE}}{{AF}} = \frac{{AM}}{{AB}}\) (2)
Từ (1) và (2) ta có: \(\frac{{AE}}{{AF}} = \frac{{MN}}{{BC}}\)
