
Cho tam giác ABC vuông tại A có đường cao AH. Gọi M, N lần lượt là trung điểm của AH, AB. Chứng minh rằng $\Delta CAM\backsim \Delta CBN$ và $\Delta CHM\backsim \Delta CAN$

+ Sử dụng kiến thức về định lý (trường hợp đồng dạng góc – góc) để chứng minh tam giác đồng dạng: Nếu hai góc của tam giác lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
+ Sử dụng kiến thức về định lý (trường hợp cạnh – góc – cạnh) để chứng minh tam giác đồng dạng: Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng với nhau.

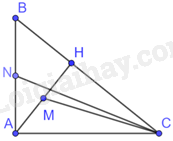
Tam giác ABC vuông tại A nên \(\widehat {BAC} = {90^0}\)
Vì AH là đường cao trong tam giác ABC nên \(AH \bot BC\).
Advertisements (Quảng cáo)
Do đó, \(\widehat {AHB} = \widehat {AHC} = {90^0}\)
Tam giác ABC và tam giác HAC có: \(\widehat {BAC} = \widehat {AHC} = {90^0},\widehat C\) chung. Do đó, $\Delta ABC\backsim \Delta HAC\left( g-g \right)$
Suy ra, \(\frac{{BC}}{{CA}} = \frac{{AB}}{{HA}} = \frac{{2BN}}{{2AM}} = \frac{{BN}}{{AM}}\) hay \(\frac{{AC}}{{CB}} = \frac{{AM}}{{BN}}\)
Tam giác CAM và tam giác CNB có:
\(\widehat {CAM} = \widehat B\left( { = {{90}^0} - \widehat {BAH}} \right),\frac{{AC}}{{CB}} = \frac{{AM}}{{BN}}\left( {cmt} \right)\)
Do đó,
Vì $\Delta ABC\backsim \Delta HAC\Rightarrow \frac{AC}{HC}=\frac{AB}{AH}=\frac{2AN}{2HM}=\frac{AN}{HM}$ hay \(\frac{{HC}}{{AC}} = \frac{{HM}}{{AN}}\)
Tam giác CHM và CAN có:\(\widehat {CHM} = \widehat {CAN} = {90^0},\;\frac{{HC}}{{AC}} = \frac{{HM}}{{AN}}\left( {cmt} \right)\)
Do đó, $\Delta CHM\backsim \Delta CAN\left( c-g-c \right)$
