
Cho tam giác ABC vuông tại A có đường cao AH.
a) Biết \(AB = 3cm,AC = 4cm,\) hãy tính độ dài các đoạn thẳng AH, BH, CH.
b) Gọi M, N lần lượt là chân đường vuông góc kẻ từ H đến AB, AC. Chứng minh rằng $\Delta HMN\backsim \Delta ABC$

a) + Sử dụng kiến thức định lí Pythagore để tìm BC: Trong một tam giác vuông, bình phương cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
+ Sử dụng kiến thức các trường hợp đồng dạng của tam giác vuông để chứng minh: Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
b) Sử dụng kiến thức các trường hợp đồng dạng của tam giác vuông để chứng minh: Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

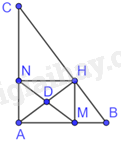
a) Tam giác ABC vuông tại A nên \(\widehat {BAC} = {90^0}\)
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A ta có: \(B{C^2} = A{B^2} + A{C^2} = {3^2} + {4^2} = 25\) nên \(BC = 5cm\)
Vì AH là đường cao trong tam giác ABC nên \(AH \bot BC\).
Do đó, \(\widehat {AHB} = \widehat {AHC} = {90^0}\)
Advertisements (Quảng cáo)
Tam giác ABC và tam giác HAC có: \(\widehat {BAC} = \widehat {AHC} = {90^0},\widehat C\) chung
Do đó, $\Delta ABC\backsim \Delta HAC\left( g-g \right)$
Suy ra: \(\frac{{AC}}{{HC}} = \frac{{BC}}{{AC}}\) nên \(CH = \frac{{C{A^2}}}{{CB}} = \frac{{{4^2}}}{5} = \frac{{16}}{5}\left( {cm} \right)\)
Do đó, \(BH = BC - CH = 5 - \frac{{16}}{5} = \frac{9}{5}\left( {cm} \right)\)
Vì $\Delta ABC\backsim \Delta HAC\left( cmt \right)$ nên \(\frac{{AB}}{{HA}} = \frac{{BC}}{{AC}}\)
Do đó, \(AH = \frac{{AB.AC}}{{BC}} = \frac{{3.4}}{5} = \frac{{12}}{5}\left( {cm} \right)\)
b) Vì \(HM \bot AB \Rightarrow \widehat {HMA} = {90^0}\), \(HN \bot AC \Rightarrow \widehat {HNA} = {90^0}\)
Tứ giác ANHM có: \(\widehat {HMA} = \widehat {NAM} = \widehat {HNA} = {90^0}\) nên tứ giác ANHM là hình chữ nhật. Do đó, \(\widehat {NHM} = {90^0}\)
Gọi D là giao điểm của hai đường chéo trong hình chữ nhật NHMA nên \(DH = DM\). Do đó, tam giác DHM cân tại D.
Suy ra, \(\widehat {DHM} = \widehat {DMH}\)
Lại có: \(\widehat {DHM} = \widehat B\left( { = {{90}^0} - \widehat {MHB}} \right)\) nên \(\widehat {DMH} = \widehat B\)
Tam giác HMN và ABC có: \(\widehat {NHM} = \widehat {BAC} = {90^0},\widehat {DMH} = \widehat B\left( {cmt} \right)\)
Do đó, $\Delta HMN\backsim \Delta ABC$(g – g)
