
Cho tứ giác ABCD như Hình 9.11. Biết rằng \(\widehat {BAD} = \widehat {BDC} = {90^0},AD = 4cm,BD = 6cm\) và \(BC = 9cm.\) Chứng minh rằng BC//AD.
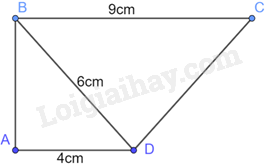
Hình 9.11

+ Sử dụng kiến thức về chứng minh hai đường thẳng song song để chứng minh BC//AD: Chứng minh hai góc ở vị trí so le trong bằng nhau là \(\widehat {BDA} = \widehat {DBC}\)
Advertisements (Quảng cáo)
+ Sử dụng kiến thức trường hợp đồng dạng của tam giác vuông để chứng minh \(\widehat {BDA} = \widehat {DBC}\): Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

Tam giác ABD và tam giác DCB có: \(\widehat {BAD} = \widehat {BDC} = {90^0},\frac{{AD}}{{BD}} = \frac{{BD}}{{BC}}\left( {do\;\frac{4}{6} = \frac{6}{9}} \right)\)
Do đó, $\Delta ABD\backsim \Delta DCB\left( ch-cgv \right)$. Suy ra: \(\widehat {BDA} = \widehat {DBC}\)
Mà hai góc này ở vị trí đồng vị nên BC//AD
