a. Cho tam giác đều ABC. Gọi M,N,P tương ứng là trung điểm của các cạnh BC, CA, AB. Chứng minh MNP là tam giác đều.
b. Cho hình vuông ABCD. Gọi M, N, P, Q tương ứng là trung điểm của các cạnh BC, CD, DA, AB. Chứng minh MNPQ là hình vuông (tứ giác đều)
c. Cho ngũ giác đều ABCDE. Gọi M, N, P, Q, R tương ứng là trung điểm của các cạnh BC, CD, DE, EA, AB. Chứng minh MNPQR là ngũ giác đều.
Giải:
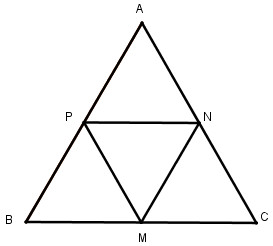
a. Ta có: M là trung điểm của BC
N là trung điểm của AC
nên MN là đường trung bình của ∆ ABC ⇒ MN = \({1 \over 2}\)AB
Ta có: P là trung điểm của AB nên MP là đường trung bình của ∆ ABC
⇒ MP = \({1 \over 2}\)AC
NP là đường trung bình của ∆ ABC ⇒ NP = \({1 \over 2}\)BC
mà AB = BC = AC (gt) ⇒ MN = MP = NP. Vậy ∆ MNP đều
b.
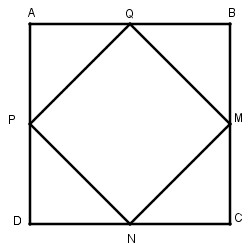
Xét ∆ APQ và ∆ BQM:
AQ = BQ (gt)
\(\widehat A = \widehat B = {90^0}\)
AP = BM (gt)
Do đó: ∆ APQ = ∆ BQM (c.g.c) ⇒ PQ = QM (1)
Xét ∆ BQM và ∆ CMN:
BM = CM (gt)
\(\widehat B = \widehat C = {90^0}\)
BQ = CN (gt)
Do đó: ∆ BQM = ∆ CMN (c.g.c) ⇒ QM = MN (2)
Xét ∆ CMN và ∆ DNP:
CN = DN (gt)
\(\widehat C = \widehat D = {90^0}\)
CM = DP (gt)
Do đó: ∆ CMN = ∆ DNP (c.g.c) ⇒ MN = NP (3)
Từ (1), (2) và (3) suy ra: MN = NP = PQ = QM
nên tứ giác MNPQ là hình thoi
Vì AP = AQ nên ∆ APQ vuông cân tại A
BQ = BM nên ∆ BMQ vuông cân tại B
\( \Rightarrow \widehat {AQP} = \widehat {BQM} = {45^0}\)
\(\widehat {AQP} + \widehat {PQM} + \widehat {BQM} = {180^0}\) (kề bù)
\( \Rightarrow \widehat {PQM} = {180^0} - \left( {\widehat {AQP} + \widehat {BQM}} \right)\)
\(= {180^0} - \left( {{{45}^0} + {{45}^0}} \right) = {90^0}\)
Vậy tứ giác MNPQ là hình vuông.
c.
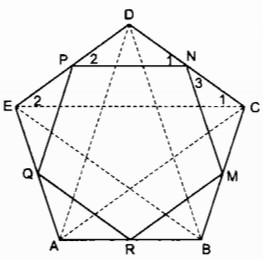
Xét ∆ ABC và ∆ BCD:
AB = BC (gt)
\(\widehat B = \widehat C\) (gt)
BC = CD (gt)
Do đó: ∆ ABC = ∆ BCD (c.g.c)
Advertisements (Quảng cáo)
⇒ AC = BD (1)
Xét ∆ BCD và ∆ CDE:
BC = CD (gt)
\(\widehat C = \widehat D\) (gt)
CD = DE (gt)
Do đó: ∆ BCD = ∆ CDE (c.g.c) ⇒ BD = CE (2)
Xét ∆ CDE và ∆ DEA:
CD = DE (gt)
\(\widehat D = \widehat E\) (gt)
DE = EA (gt)
Do đó: ∆ CDE = ∆ DEA (c.g.c) ⇒ CE = DA (3)
Xét ∆ DEA và ∆ EAB:
DE = EA (gt)
\(\widehat E = \widehat A\) (gt)
EA = AB (gt)
Do đó: ∆ DEA = ∆ EAB (c.g.c) ⇒ DA = EB (4)
Từ (1), (2), (3), (4) suy ra: AC = BD = CE = DA = EB
Trong ∆ ABC ta có RM là đường trung bình
⇒ RM = \({1 \over 2}\)AC (tính chất đường trung bình của tam giác)
Mặt khác, ta có: Trong ∆ BCD ta có MN là đường trung bình
⇒ MN = \({1 \over 2}\)BD (tính chất đường trung bình của tam giác)
Trong ∆ CDE ta có NP là đường trung bình
⇒ NP = \({1 \over 2}\)CE (tính chất đường trung bình của tam giác)
Trong ∆ 9DEA ta có PQ là đường trung bình
⇒ PQ = \{1 \over 2}\)DA (tính chất đường trung bình của tam giác)
Trong ∆ EAB ta có QR là đường trung bình
⇒ QR = \({1 \over 2}\)EB (tính chất đường trung bình của tam giác)
Suy ra: MN = NP = PQ = QR = RM
Ta có: \(\widehat A = \widehat B = \widehat C = \widehat D = \widehat E = {{\left( {5 - 2} \right){{.180}^0}} \over 5} = {108^0}\)
∆ DPN cân tại D
\( \Rightarrow \widehat {DPN} = \widehat {DNP} = {{{{180}^0} - \widehat D} \over 2} = {{{{180}^0} - {{108}^0}} \over 2} = {36^0}\)
∆ CNM cân tại C
\( \Rightarrow \widehat {CNM} = \widehat {CMN} = {{{{180}^0} - \widehat C} \over 2} = {{{{180}^0} - {{108}^0}} \over 2} = {36^0}\)
\(\widehat {ADN} + \widehat {PNM} + \widehat {CNM} = {180^0}\)
\( \Rightarrow \widehat {PNM} = {180^0} - \left( {\widehat {ADN} + \widehat {CNM}} \right)\)
\(= {180^0} - \left( {{{36}^0} + {{36}^0}} \right) = {108^0}\)
∆ BMR cân tại B
\(\eqalign{ & \Rightarrow \widehat {BMR} = \widehat {BRM} = {{180^\circ - \widehat B} \over 2} = {{180^\circ - 108^\circ } \over 2} = 36^\circ \cr & \widehat {CMN} + \widehat {NMR} + \widehat {BMR} = 180^\circ \cr & \Rightarrow \widehat {NMR} \cr &= 180^\circ - \left( {\widehat {CMN} + \widehat {BMR}} \right) \cr & = 180^\circ - \left( {36^\circ + 36^\circ } \right) = 108^\circ \cr} \)
∆ ARQ cân tại A
\(\eqalign{ & \Rightarrow \widehat {ARQ} = \widehat {AQR} = {{180^\circ - \widehat A} \over 2} = {{180^\circ - 108^\circ } \over 2} = 36^\circ \cr & \widehat {BRM} + \widehat {MRQ} + \widehat {ARQ} = 180^\circ \cr & \Rightarrow \widehat {MRQ} = 180^\circ - \left( {\widehat {BRM} + \widehat {ARQ}} \right) \cr & = 180^\circ - \left( {36^\circ + 36^\circ } \right) = 108^\circ \cr} \)
∆ QEP cân tại E
\(\eqalign{ & \Rightarrow \widehat {EQP} = \widehat {EPQ} = {{180^\circ - \widehat E} \over 2} = {{180^\circ - 108^\circ } \over 2} = 36^\circ \cr & \widehat {AQR} + \widehat {RQP} + \widehat {EQP} = 180^\circ \cr & \Rightarrow \widehat {RQP} = 180^\circ - \left( {\widehat {AQR} + \widehat {EQP}} \right) \cr & = 180^\circ - \left( {36^\circ + 36^\circ } \right) = 108^\circ \cr & \widehat {EPQ} + \widehat {QPN} + \widehat {DPN} = 180^\circ \cr & \Rightarrow \widehat {QPN} = 180^\circ - \left( {\widehat {EPQ} + \widehat {DPN}} \right) \cr & = 180^\circ - \left( {36^\circ + 36^\circ } \right) = 108^\circ \cr} \)
Suy ra : \(\widehat {PNM} = \widehat {NMR} = \widehat {MRQ} = \widehat {RQP} = \widehat {QPN}\)
Vậy MNPQR là ngũ giác đều.
