Cho hình vuông ABCD có AB = 3cm
Trên tia đối của tia BA lấy điểm K sao cho BK = 1cm
Trên tia đối của tia CB lấy điểm L sao cho CL = 1cm
Trên tia đối của tia DC lấy điểm M sao cho MD = 1cm
Trên tia đối của tia AD lấy điểm N sao cho NA = 1cm
Chứng minh KLMN là hình vuông
Giải:
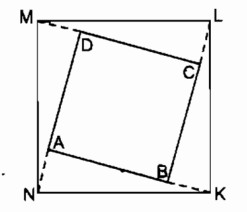
Xét ∆ ANK và ∆ BKL :
AN = BK (gt)
\(\widehat A = \widehat B = 90^\circ \)
AK = BL (vì AB = BC, BK = CL)
Do đó ∆ ANK = ∆ BKL (c.g.c)
⇒ NK = KL (1)
Xét ∆ BKL và ∆ CLM:
BK = CL (gt)
Advertisements (Quảng cáo)
\(\widehat B = \widehat C = 90^\circ \)
BL = CM (vì BC = CD, CL = DM)
Do đó: ∆ BKL = ∆ CLM (c.g.c)
⇒ KL = LM (2)
Xét ∆ CLM và ∆ DMN :
CL = DM (gt)
\(\widehat C = \widehat D = 90^\circ \)
CM = DN (vì CD = DA, DM = AN)
Do đó: ∆ CLM = ∆ DMN (c.g.c)
⇒ LM = MN (3)
Từ (1), (2) và (3) ⇒ NK = KL = LM = MN
Tứ giác MNKL là hình thoi
∆ ANK = ∆ BKL \( \Rightarrow \widehat {ANK} = \widehat {BKL}\)
Trong tam giác ANK có \(\widehat A = 1v \Rightarrow \widehat {ANK} + \widehat {AKN} = 90^\circ \)
\( \Rightarrow \widehat {BKL} + \widehat {AKN} = 90^\circ \)hay \(\widehat {NKL} = 90^\circ \)
Vậy tứ giác MNKL là hình vuông.
